三角関数

← PC版は別頁

== 三角関数(3) ==
○　三角関数のグラフと最大，最小

(1)　y=sinx のグラフは，表1により，点をなめらかに結べば得られる．

　特に，「原点を通ること」「−1≦sin x≦1となること」が重要である．

表1

･･･

$\frac{\pi}{6}$

$\frac{\pi}{4}$

$\frac{\pi}{3}$

$\frac{\pi}{2}$

$\frac{2\pi}{3}$

$\frac{3\pi}{4}$

$\frac{5\pi}{6}$

$\pi$

$\frac{7\pi}{6}$

･･･

sinx

･･･

$\frac{1}{2}$

$\frac{1}{\sqrt{2}}$

$\frac{\sqrt{3}}{2}$

$\frac{1}{\sqrt{2}}$

$\frac{1}{2}$

$-\frac{1}{2}$

･･･

(2)　y=cosx のグラフも同様にして，表2により，点をなめらかに結べば得られる．

　特に，「x=0のときy=1になること」「 −1≦cos x≦1となること」が重要である．

表2

･･･

$\frac{\pi}{6}$

$\frac{\pi}{4}$

$\frac{\pi}{3}$

$\frac{\pi}{2}$

$\frac{2\pi}{3}$

$\frac{3\pi}{4}$

$\frac{5\pi}{6}$

$\pi$

$\frac{7\pi}{6}$

･･･

cosx

･･･

$\frac{\sqrt{3}}{2}$

$\frac{1}{\sqrt{2}}$

$\frac{1}{2}$

$-\frac{1}{2}$

$-\frac{1}{\sqrt{2}}$

$-\frac{\sqrt{3}}{2}$

−1

$-\frac{\sqrt{3}}{2}$

･･･

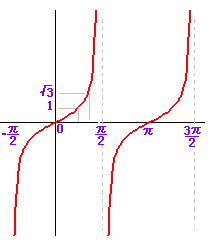
(3)　y=tanx のグラフも同様であるが，このグラフは他の２つと全く異なり，取り得る値の範囲が
−∞<tanx<∞ となるところが特徴．
　特に，− <x<の区間だけで，y は全実数値を取る．

例と答
(1)　y=2sinx+3 　(-≦x≦) の最大値，最小値を求めよ．

（答案）
t=sinx とおくと，
y=2t+3　(−1≦t ≦1）
t=−1 (x=−) のとき最小値 1 をとる．
t=1 (x = ) のとき最大値 5 をとる．

(2)　y=cos²x−2cosx 　(0≦x≦π) の最大値，最小値を求めよ．

（答案）
t=cosx とおくと，
y=t²−2t　(−1≦t≦1）
y=(t−1)²−1　だから
t=−1 (x= π) のとき最大値 3 をとる．
t=1 (x = 0) のとき最小値 -1 をとる．

(3)　y=−2 tan²x−4 tanx 　(−≦x≦) の最大値，最小値を求めよ．

（答案）
t=tanx とおくと，
y=−2t² -4t 　(−∞<t<∞）
y=−2(t +1)²+2　だから
最小値　なし
t=−1 (x =−) のとき最大値 2 をとる．

■即答問題■

　次の関数の最大値，最小値を求めよ．ないときは，「　*　」と書け．（最大値，最小値を与えるxの値は省略してよい．）
(1)　 y=− 3 sinx+5 　(−≦x≦) (2)　y=cos²x+4cosx + 3 　(0≦x≦π)

(3)　y=4 tan²x−4 tanx 　(−≦x≦)

○　三角関数の微分

　［　要点　］
　y=sinx　→　y’=cosx　･･･(1)
　y=cosx　→　y’=−sinx　･･･(2)

　 y=tanx　→　y’=　･･･(3)

　なお，上の結果に合成関数の微分法を組み合わせた，次の公式はよく登場する．
　y=sin kx　→　y’=kcos kx
　y=cos kx　→　y’=−ksin kx　など

(証明)
　三角関数の微分（導関数）を求めるとき，右の極限値を利用する．
(1)←：
y=sinx　→　y’=

= =

　ここで，cos(x +)→cosx, →1
だから，y’=cosx

(2)←：も同様にして示される．
(3)←：y=tanxのとき
商の微分法により　y’=

=

（重要な極限値）

この式は，通常，次のような図を用いて示される．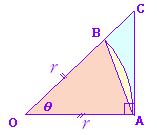

△OAB＜扇形OAB＜△OACだから
ア） θ＞0のとき

　　r2sinθ＜r2θ＜r2tanθ

　　0＜sinθ＜θ＜tanθ

　　0＜1＜＜cosθ→ 1 (θ→0 のとき)　だから

　　 → 1 (θ→0 のとき)

イ）θ＜0のとき，θ=−t とおくと

　　 ==→ 1 (θ→0 のとき)

ア）イ）より，=1

例と答
　次の関数を微分せよ．
(1)　y=sin 2x
　　（答案）　y=sin t
　　　　　　　　　 t=2x
　　　　　　　----------------
　　　==sin t×2 =2 sin 2x･･･(答)

(2)　y=cos2x
　　（答案）y=t2
　　　　　　　　 t=cosx
　　　　　　　----------------
　　　==2t(−sinx)=−2cosx sinx･･･(答)

(3)　y=tan(3x+2)
　　（答案）　y=tan t
　　　　　　　　　　 t=3x+2
　　　　　　　----------------
　==×3 =･･･(答)

■即答問題■

　次の関数を微分せよ．
(1)　y=sin(− 3x+2) (2)　y=tan(2x-3)

(3)　y=cos³4x 　　　y=t³
　　　　　　t=cos p
　　　　　　　　　p=4x
------------------------------------
　　　= =3t2·(−sin p)·4

→閉じる←

○･･･メニューに戻る