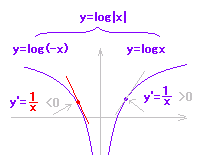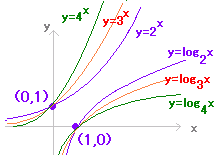
|
例1 y=2x+1･･･(1)を x について解くと， x=･･･(2) x，y を入れ替えると y=･･･(3) このとき，(3)を(1)の逆関数という． 例2 y=ex･･･(1)を x について解くと， x =loge y･･･(2) x，y を入れ替えると y=loge x･･･(3) このとき，(3)を(1)の逆関数という． 一般に， y=f(x)･･･(1)を x について解いたものを x=f−1(y)･･･(2)と書く． x，y を入れ替えると y=f−1(x)･･･(3) このとき，(3)を(1)の逆関数という． |
| (1)と(2)は同じものであるが(2)と(3)は逆関数 (1)と(2)’は逆関数であるが(2)’と(3)は同じもの （どちらが先でもよい）   ※y=f(x)を変形して x=f −1(y)にしたら逆関数になるわけではない．上の(1)(2)は同じもの（いつでも元に戻せる．） x，y を入れ替えたときに対応関係が逆になる．（当然のこと） ※x，y を入れ替えると縦と横が入れ替わるので，y=x の直線に関して対称移動したものになる． |
| ○逆関数の性質 ある関数 y=f(x) と，その逆関数 y=f −1(x) とでは (1)グラフはy=x の直線に関して対称になる． (2)定義域と値域が入れ替わる． |
 (1)(2)は同じものなので y=f(x) (a≦x≦b) (α≦y≦β)･･･(1)のとき x=f −1(y) (a≦x≦b) (α≦y≦β)･･･(2) x，y を入れ替えると y=f −1(x) (a≦y≦b) (α≦x≦β)･･･(3) |
| ○対数関数のグラフ 対数関数 y=loga xは，指数関数 y=ax の逆関数となっているので，各々のグラフはy=x の直線に関して対称となっている． また，y=ax(-∞<x<∞)(0<y<∞)の定義域と値域を入れ替えると，y=loga x(0<x<∞)(-∞<y<∞) 特に，y=axがつねに(0，1) を通るのに対応して，y=loga xはつねに(1，0) を通る． |
 y=axの値域はy>0→ y=loga xの定義域はx>0 |
| 指数関数とその逆関数となっている対数関数のグラフを２，３示すと次の図のとおり． |
 |
| ○対数関数の微分 底が e (自然対数の底 2.71828･･･)の対数は，自然対数と呼ばれ，底を省略してよい．log x は logex を表わす． [要点] y=log x(底はe)→y’= （証明) y=log xのとき， y’== == (2) = （y=logax の微分は，底の変換をすれば上の公式でできる．) |
| ［指数関数，対数関数の微分に使う重要な極限値］ 次の3つの極限は，互いに同値であることが知られている．（証明略) (1)=1 (2)=1 (3)(1+h)=e |
| 例と答 次の関数を微分せよ．（各々の定義域は真数が正の数となる区間とする．) (1)y=log3x→ y=log3+logx→y’= （別解) t =3xとおくと y=log t t =3x ------------- 合成関数微分法により = =×3=×3= (2)y=log10x→y = →y’= (3)y=log(x2+x+1) y=log t t =x2+x+1 ------------- 合成関数微分法により = =×(2x+1)= |
(4)y=log|x| ア) x > 0のとき，y’= イ) x < 0のとき，y=log(-x) y=logt t =-x ------------- 合成関数微分法により = =×(-1)=×(−1)= 以上から，y=log|x|→y’= ただし，グラフは次のようになっている．  |
| ■短答問題■ |