|
○ 積の微分法 関数 y =f(x),y =g(x)の導関数が分かっているとき,これらの関数の積 y =f(x)g(x) の導関数を f(x),g(x),f’(x),g’(x) で表わす公式を求める. ◇積の微分法の公式◇ ◇これを用いれば3個の積についても,公式を作ることができる. (∵ (fgh)’=(fg)’h+(fg)h’=(f’g+fg’)h+(fg)h’ = f ’gh+fg’h+fgh’) |
(証明) |
|
スマホ画面の横幅が,教材の横幅と少し合わないときは,リンクの掛かっていない文字[例えばこの文字]をトントンとたたくと合うようです(ダブルクリック,ダブルタップ)
このページでは,個々の関数の微分が分かるときに,それらの関数の積,商,合成関数,逆関数で表わされる関数の微分を求める方法を学ぶ. |
| (必要となる場面) (1) y = x+1の微分はy’=1,y = x2+1の微分はy’=2x ・・それでは,y = (x+1)(x2+1) の微分は? (2) y = xの微分はy’=1,y = x2 + 1の微分はy’=2x ・・それでは,y = の微分は? (3) y = x3の微分はy’=3x2,y = x2 + 1の微分はy’=2x ・・それでは,y = (x2+ 1)3 の微分は? |
|
○ 積の微分法 関数 y =f(x),y =g(x)の導関数が分かっているとき,これらの関数の積 y =f(x)g(x) の導関数を f(x),g(x),f’(x),g’(x) で表わす公式を求める. ◇積の微分法の公式◇ ◇これを用いれば3個の積についても,公式を作ることができる. (∵ (fgh)’=(fg)’h+(fg)h’=(f’g+fg’)h+(fg)h’ = f ’gh+fg’h+fgh’) |
(証明) |
| 例と答 (1) y = x の微分はy’=1,y = x2 の微分はy’=2x であるから,y = x・ x2 すなわち y = x3 の微分は y’=1・x2+x・2x = x2+2x2 = 3x2 (2) y = x の微分はy’=1,y = x3 の微分はy’=3x2 であるから,y = x・x3 すなわち y = x4 の微分は y’=1・x3+x・3x2 = x3+3x3 = 4x3 (*) 一般に,1≦k≦nとなる整数kについて, y = xk についてy’=kxk−1 が成り立つならば, y = xk+1 の微分は y’=(x・xk)’=1・xk+x・kxk−1=xk+kxk=(k+1)xk となるから,すべての正の整数nについて, |
(4) y = (x2+1)(x3+1) の微分を求めよ.y’= 2x(x3+1)+ (x2+1)3x2(5) y = x(x+1)(x+2) の微分を求めよ. y’= (x+1)(x+2)+x(x+2)+x(x+1) |
| ■短答問題■ 次の関数の導関数を求めよ. (空欄に半角数字を書き込むこと) (1) y =(2x2+3)(3x2+4) |
| (2) y =(x+1)(x+2)(x+3) |
| ○ 商の微分法 関数y=f(x),y=g(x)の導関数が分かっているとき,これらの商 y=
の導関数を f(x),g(x),f’(x),g’(x) で表わす公式を求める. ◇商の微分法の公式◇ y = → y’=
|
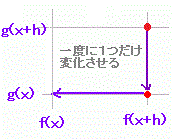 (証明) (証明)ここで,次のように変形する これにより |
| 例と答 次の関数の導関数を求めよ. (1) y = (答案) y’= = = |
|
(2)
y =
(答案) y’= = = |
| ■短答問題■ 次の関数の導関数を求めよ. (半角数字で記入すること) (1) y = (2) y = |
(3) y = (4) y = |
| ○ 合成関数の微分法 関数 y = f(g(x)) を y = f(t) と t = g(x) の合成関数と考えるとき, =
3個の関数を合成した場合も,同様 =
|
| (証明) はを略したものであるが,平均変化率 は 有限値÷有限値の,普通の分数であるので, =
のように変形することができる. 次に Δx → 0 の極限を考えるとき,Δt → 0 となる(以下,不連続関数を用いた変換は考えない)ことに注意すると, = ·
だから
= |
| 例と答 次の関数の導関数を求めよ. (1) y =(2x+3)4 y =t4 |
(2) y =(x2+x+1)3
y =t3 |
| ■短答問題■ 次の関数の導関数を求めよ. (空欄に半角数字を書き込むこと) (1) y = (4x−3)5 |
| (2) y = (x2−x+2)4
|
| ○ 逆関数の微分法 xがyの関数として表わされているとき,yをxで微分するには,xをyで微分したものの逆数を取ればよい.(この場合,導関数がyの関数で表わされることもある.) = (ただし,≠0 ) |
| (証明) 微分可能な関数では,Δx → 0のとき,Δy → 0だから, = = =
|
| 例と答 (1) y= (0<x) y2=xだから
= == ・・・(答) |
(2) 対数関数の微分は,次のように指数関数の微分を用いて計算することもできる.
y=log x ⇔ x=ey |
| ○ 陰関数の微分法 y=2x+1のようにyについて解かれた形になっているものを陽関数,x2+y2=1のようにx,yの関係式で示され,y について解かれた形になっていないものを陰関数という. 陰関数で表わされているものを微分するには,右の例のように両辺をそのまま微分すればよい. yはxの関数と考えて微分する. |
| 例 x2+y2=1 両辺をx で微分すると, (x2+y2)=(1)
2x+(y2)=0 2x+2y=0 =− (陰関数の微分は,yも用いて表わせばよい.) |
| ■短答問題■ 次の関係式から を求めよ.(結果はy も用いて表わしてもよい.) (空欄には半角英数字を書き込むこと) (1) x2+ xy+y2=1 |
|
(2) 2x2−y2=1
|