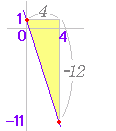
|
スマホ画面の横幅が,教材の横幅と少し合わないときは,リンクの掛かっていない文字[例えばこの文字]をトントンとたたくと合うようです(ダブルクリック,ダブルタップ)
○ はじめに平均変化率の極限値が微分係数f ’(a)で,微分係数の定義における定数aを変数 xに変えたものが導関数(微分)f ’(x)なので,次の流れ図に沿って解説する. |
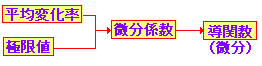 |
| ○ 平均変化率 中学校で「変化の割合」と呼ばれるものは,高校では「平均変化率」と呼ばれる. ( 平均変化率 ) =
一般に,関数 y = f(x) の区間 a≦x≦b における平均変化率は で定義される.  |
||||
例
|
| ■即答問題■ 次の各関数の与えられた区間における平均変化率を求めよ.(正しい選択肢をクリック) (1) y =2x−1 (0≦x≦3) [ 選択肢 ] 0 1 2 3 4 5 6 7 8 9(2) y =x2 (0≦x≦4) [ 選択肢 ] 0 1 2 3 4 5 6 7 8 9 |
(3) y =x3 (-1≦x≦2)
[ 選択肢 ] 0 1 2 3 4 5 6 7 8 9(4) y =2x2+x (-1≦x≦1) [ 選択肢 ] 0 1 2 3 4 5 6 7 8 9 |
| ○ 極限値 (はじめに) 関数値 ----- 右図 1) は ( 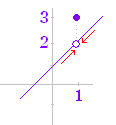 図1)
図1)関数値 極限値 右図 2) は ( 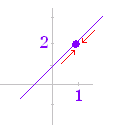 図2)
図2)関数値 極限値 右図 3) は (  図 3)
図 3)関数値 極限値 以上の1)2)3)の違いから分かるように,xが限りなく1 に近づくときの f(x) の値(これを極限値という)は,関数値 f(1)とは無関係で,xが1 でないときの1 付近の値で決まる. |
|
(極限値の定義)
関数 f(x) において,x が a と異なる値をとりながら a に限りなく近づくとき, f(x) が一定の値 b に限りなく近づくとき, x → a のときの f(x) の極限値は b であるといい ※ 「xがaと異なる値をとりながら」という条件は次のようにはたらく. x≠1のとき は約分できて x + 1 となるので 約分する前は代入できないが,約分後は単なる代入と同じ. |
|
※ 繰り返しになるが, 例 1)において, 例 3)も同様 例 2)は,定義によって「たまたま」 g(1)=2 となっている. ※ 数学専攻の人が精密な証明をするときを除けば,「限りなく近づく」とは何かということに深入りせずに,直感的に理解するとよい. |
|
関数の極限については,次の公式の組合わせてできるものが求められればよい.
(Ⅰ) (Ⅱ) (Ⅲ) |
| 例と答 (1) (2) (3) |
| ■即答問題■ 次の極限値を求めよ.(正しい選択肢をクリック) (1) [ 選択肢 ] 0 1 2 3 4 5 6 7 8 9(2) [ 選択肢 ] 0 1 2 3 4 5 6 7 8 9(3) [ 選択肢 ] 0 1 2 3 4 5 6 7 8 9(4) [ 選択肢 ] 0 1 2 3 4 5 6 7 8 9 |
| ○ 不定形の極限 分母が0,分子も0の「0÷0の形」となる. このように,元の式に直接値を代入すると「0÷0形」になるものを不定形の極限という. 不定形の極限は,見かけは不定の形をしているが,不定である原因を取り除けば,極限値は求まり,結果は不定ではない. ここで重要となるのが,「xがaと異なる値をとりながら」という条件で, |
| ※ 0÷0の形の式を不定形という. (i) 数学で次の方程式は「解なし」「不能」となる. 0x=3 (正しくない変形だが) x = この形の式を「不能形」という. (ii) 次の方程式は「任意の数」「不定」となる. 0x=0 (正しくない変形だが) x = この形の式を「不定形」という. ※ いわゆる「不定形の極限」には,0÷0形以外に,∞-∞形,0×∞形などがあるが,ここでは微分係数・導関数を理解する上で必要な0÷0形のみを取り上げる. |
| 例と答・・・約分により分母,分子が0になる原因(因数)を取り除くところがポイント (1) (2) |
| (3) (4) |
| ■即答問題■ 次の極限値を求めよ.(正しい選択肢をクリック) (1) [ 選択肢 ] 0 1 2 3 4 5 6 7 8 9(2) [ 選択肢 ] 0 1 2 3 4 5 6 7 8 9 |
(3)
[ 選択肢 ] 0 1 2 3 4 5 6 7 8 9(4) [ 選択肢 ] -4 -3 -2 -1 0 1 2 3 4 5 |
| ○ 微分係数の定義 関数 y=f(x) の区間 a≦x≦b における平均変化率は, すなわち, |
※ 区間 a≦x≦b の幅を限りなく0に近づけると 平均変化率 の式において, 分母,分子とも限りなく0に近づくが,平均変化率の極限値は0になるのでなく,上に述べたようにいわゆる不定形の極限となり,有限確定値となる. また,この極限値f ’(a)は点A(x=a)における接線の傾きとなる. |
|
例1 f(x) =x2のときx=1における微分係数f’(1)は または 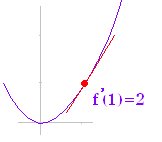 |
| 例2 f(x)=x3のときx=1における微分係数f’(1)は 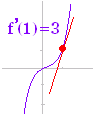 |
| 例3 [重要例題] f(x)=x2のときx=aにおける微分係数f’(a)は  |
| ■短答問題■ (半角英数字で答えること) 次の微分係数を定義に従って計算せよ. (1) f(x)=2x+3のときf’(1) (2) f(x)=3x2+4のときf’(0) (3) f(x)=x2+x+2のとき f’(2) |
|
○ 導関数(微分)の定義 各々の定数aに対して定義される微分係数 を,aに対して微分係数f’(a)を対応させる関数と考えたものを導関数という. 導関数f’(x)は,元の関数の微分とも呼ばれる.また,導関数を求めることを微分するという. ○ 導関数(微分)と微分係数の関係 導関数が求まると,導関数にxの値を導入するだけで微分係数が求まるので,個々の定数aに対して f’(a)を求める煩雑な手続きは不要となる.○ 導関数(微分)を表わす記号 微分法は,ニュートンとライプニッツが別々に考え出したと言われており,微分を表わす記号もニュートンの記号とライプニッツの記号がある.各々長所があり,両方とも使われる. ニュートンの記号:y’ ,f’(x) ライプニッツの記号:,f(x)ライプニッツの記号は,Δy=f(x + h)−f(x),Δx=h として, 平均変化率をで表わすとき,導関数の定義を |
| 例と答 次の関数の導関数を求めよ.(次の関数を微分せよ.)また,与えられたxの値に対する微分係数を求めよ. (1) f(x)=x2,f’(1)
x=1を代入するとf’(1)=2(2) f(x)=x3,f’(2) x=2を代入するとf’(2)=12
|
| ■短答問題■ (半角英数字で答えること) 次の関数の導関数を定義に従って計算せよ. (1) f(x)=2x2 (2) y=−3x+4 |