|
○ はじめに 多項式の展開とは異なり,三角関数において( )をはずす変形は簡単ではない.例えば,次のような変形はできない. |
|
○ はじめに 多項式の展開とは異なり,三角関数において( )をはずす変形は簡単ではない.例えば,次のような変形はできない. |
| ○ 三角関数の加法定理
[要点]
図において,∠AOB=α,∠BOC=β,AO=1とするとき,点Aのx座標がcos(α+β),y座標がsin(α+β)となる. x=OE=OC−BD=cosα cosβ−sinαsinβ→(1) y=AE=AD+DE=sinαcosβ+cosαsinβ→(2)
公式(1)(2)は必ず言えるようにし,残りは短時間に導けるようにする.(何度も使ううちに(3)以下を覚えてしまっても構わない.) |
|
(3)(4)の証明 (3)←
引き算は符号が逆の数の足し算と同じ
(4)←
引き算は符号が逆の数の足し算と同じ
(5)(6)の証明 (5)←
三角関数の相互関係:
(1)(2)の結果を使う
分母分子を
(6)←
引き算は符号が逆の数の足し算と同じ
(5)の結果を使う
…(6)証明終わり■ |
次の図において,下半分の桃色の三角形の辺の長さの比を,上半分の水色の三角形の比で表すと,偶関数・奇関数の性質が分かる.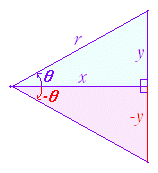 |
|
即答問題 次の各式と等しいものを下から選べ.
はじめに上の式を選び,続いて下の式を選べ.(合っていれば消える.) cos(α+β) sin(α−β) cos(α−β) cos(45°+30°) cos(60°+45°) sin(60°+ 45°) [ 完 ] |
|
○ 倍角公式
[要点]
|
|
(証明) sin(α+β)=sinα cosβ+cosα sinβ・・・(1) において,α=βとおくと, sin2α=2sinα cosα →(7) cos(α+β)=cosα cosβ−sinαsinβ・・・(2) において,α=β とおくと, cos2α=cos2α−sin2α →(8) (8)においてsin2α=1−cos2αを代入すると, cos2α=2cos2α−1 →(9) (8)においてcos2α=1−sin2αを代入すると, cos2α=1−2sin2α →(10) tan(α+β)= ・・・(5) において,α=β とおくと, tan2α= →(11) |
|
○ 半角公式
[要点]
半角公式は,次の形で示されることもある.±は,象限に応じて一方の符号を選ぶことを表わす. |
|
(9)(10)を変形すれば→(12)(13) (12)÷(13)により→(14) |
|
○ 3倍角公式 2倍角公式と加法定理を組み合わせると,次の公式ができる.
[要点]
(15)←sin(2α+α)=sin2α cosα+cos2α sinα =2sinαcos2α+(1−2sin2α)sinα =2sinα ( 1−sin2α)+(1−2sin2α)sinα =3sinα −4sin3α …(15)証明終わり■ (16)← cos(2α+α)=cos2α cosα−sin2α sinα =(2cos2α−1 )cosα−2sin2α cosα =(2cos2α−1 )cosα−2(1−cos2α) cosα =4cos3α−3cosα …(16)証明終わり■ (17)←
|
|
|

|
|
○ 積和の公式(積を和に直す公式)
[要点]
sinα cosβ={sin(α+β)+sin(α − β)}・・・(18)
cosα sinβ={sin(α+β)−sin(α−β)}・・・(19) cosα cosβ={cos(α+β)+cos(α−β)}・・・(20) sinα sinβ=− {cos(α+β)−cos(α−β)}・・・(21) ○ 和積の公式(和を積に直す公式)
[要点]
sinA+ sinB = 2 sincos・・・(22)
sinA−sinB = 2 cossin・・・(23) cosA+ cosB = 2 coscos・・・(24) cosA−cosB=−2 sinsin・・・(25) |
|
(証明)
sin(α+β)=sinα cosβ+cosα sinβ・・・(1) +) sin(α−β)=sinα cosβ−cosα sinβ・・・(3) -------------------------- sin(α+β)+sin(α−β)=2sinα cosβ→(18) sin(α+β)=sinα cosβ+cosα sinβ・・・(1) −) sin(α−β)=sinα cosβ−cosα sinβ・・・(3) -------------------------- sin(α+β)−sin(α−β)= 2cosα sinβ→(19) cos(α+β)=cosα cosβ - sinα sinβ・・・(2) +) cos(α−β)=cosα cosβ+ sinα sinβ・・・(4) -------------------------- cos(α+β)+cos(α−β)=2cosα cosβ→(20) cos(α+β)=cosα cosβ - sinα sinβ・・・(2) −) cos(α−β)=cosα cosβ+ sinα sinβ・・・(4) -------------------------- cos(α+β)−cos(α−β)= −2sinα sinβ→(21) (18)〜(21)において,α+β=A,α−β=Bとおくと, α=,β=→(22)〜(25) |
|
− 2sin(α+β)sin(α−β) 2cos(α+β)cos(α−β) 2sin 2cos 
|