数列

■数列とその和

スマホ画面の横幅が，教材の横幅と少し合わないときは，リンクの掛かっていない文字［例えばこの文字］をトントンとたたくと合うようです（ダブルクリック，ダブルタップ）

○　数列

　何らかの規則に従って，数を一列に並べたものを数列という．
　数列を記号で表わすときは，第1項を a₁，第2項を a₂，第3項を a₃，…のように添字を付けて表わす．
　第n項がa_nであるような数列のことを，単に数列｛a_n｝と書く．

例1　数列｛a_n｝が2，4，6，8，···　のとき，
a₁=2，a₂=4，a₃=6，a₄=8　となる．

例と答
　次の数列について，なるべく簡単な規則を見つけて空欄を埋めよ．
(1)　1，4，7，10，[ 　]，16，…答13（3ずつ加える）
(2)　50，45，40，35，[　 ]，…答30（5ずつ引く）
(3)　1，2，4，8，[　 ]，…答16（2ずつ掛ける）
(4)　1，4，9，16，[　 ]，…答25(1,2,3,...の2乗を考える)
(5)　2，6，12，20，30，[　 ]，…答42（n(n+1)を考える）

○　数列の一般項

　数列の第n項をnの式で表わしたものを一般項という．

例2　数列｛a_n｝：　2，4，6，8，…　の一般項をｎの１次式で表わすと a_n=2n (ｎ=1，2，3，…）となる．
例3　数列｛b_n｝の一般項が b_n=2n − 1 (ｎ=1，2，3，…）のとき，数列｛b_n｝は　1，3，5，…　となる．

　数列の添字は何番目の項であるかを表わす単なる記号なので，計算方法が定まっている累乗記号と区別することが重要．
例4　x_n=2n + 1 のとき，x_n²=(2n + 1)²
例5　y_n=n² − 1 のとき，y₅=25 − 1 = 24

例と答
I)
　一般項が次の式で与えられる数列について，［　］内に示した項を求めよ．
(1)　a_n=n(n − 3)　　…　→　［第5項］　答 a₅=10
(2)　x_n=2ⁿ⁺¹　　…　→　［第3項］　答 x₃=16

II)
　次の数列について，なるべく簡単な規則を見つけて一般項を求めよ．
(1)　｛a_n｝：20，18，16，14，…　→　答　a_n=22 − 2n
(2)　｛b_n｝：1，3，9，27，…　→　答　b_n=3ⁿ⁻¹
(3)　｛x_n｝：1·3，3·5，5·7，7·9，…　→　答　x_n=(2n−1)(2n+1)

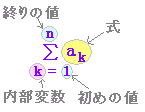
○　数列の和

　次の公式が成り立つ．
(0)　k + k + k + ··· + k (n個の和)=nk

(1)　1 + 2 + 3 + ···+ n =

(2)　1² + 2² + 3² + ···+ n²=

(3)　1³ + 2³ + 3³ + ···+ n³={}2

　初項a ，公比ｒ（≠1），項数n の等比数列の和は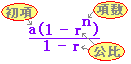

だから
(4)　a + ar + ar² + ar³ + ···+ arⁿ⁻¹=

※初項a，公比r（≠1），項数nの等比数列の一般項は
a_n = arⁿ⁻¹であるが，和の方はrⁿ が登場する．

例と答
(0)　5 + 5 + 5 + ··· + 5 (n個の和)=5n

(1)　1 + 2 + 3 + ···+ 100==5050

(2)　1² + 2² + 3² + ···+ 10²==385

(3)　1³ + 2³ + 3³ + ···+ 9³= {}²= 2025

※　等比数列の和は，初項，公比，項数に分けて読み取ると簡単

(4)　1 + 2 + 4 + 8 + 16 + 32
初項1，公比2，項数6の等比数列の和だから

=63

(5)　2 + 6 + 18 + 54 + 162
初項2，公比3，項数5の等比数列の和だから

=242

(6) 　(x+1) + (x+1)² + (x+1)³ + ··· + (x+1)ⁿ
ただしx≠0
初項(x+1)，公比(x+1)，項数nの等比数列の和だから

○　和の記号Σ
　
(1)　Σ記号は，「内部変数」に指定された文字を，「初めの値」から「終りの値」まで１ずつ増やして，「式」で示される項を順に加えたものを表わす．

例6
$\sum_{k=1}^5a_k=a_1+ a_2+ a_3+ a_4+ a_5$
$\sum_{k=1}^4b_k=b_1+ b_2+ b_3+ b_4$
$\sum_{k=2}^6x_k=x_2+ x_3+ x_4+ x_5+ x_6$

(2)　内部変数はΣ記号を和に直すと残らないので，内部変数がどのような文字で表わされているかは結果に影響しない．
　また，内部変数に指定された文字以外の文字や数字は変化させない．

例7

$\sum_{k=1}^5k=1+ 2+ 3+ 4+ 5$
$\sum_{j=1}^5k=1+ 2+ 3+ 4+ 5$

$\sum_{k=1}^5kn=1n+ 2n+ 3n+ 4n+ 5n$

(3)　Σ記号を用いると上に述べた数列の和の公式は，次の形に書くことができる．

　　　 $\sum_{k=1}^nk=\frac{n(n+ 1)}{2}$
　　　 $\sum_{k=1}^nk^2=\frac{n(n+ 1)(2n+ 1)}{6}$
　　　 $\sum_{k=1}^nk^3=\{\frac{n(n+ 1)}{2}\}^2$
　　　 $\sum_{k=1}^nar^{k-1}=\frac{a(1-r^n)}{1-r}$

例8
$\sum_{k=1}^{100}k=\frac{100(100+ 1)}{2}=5050$
$\sum_{k=1}^{n+ 1}k^2=\frac{(n+ 1)(n+ 2)(2n+ 3)}{6}$
$\sum_{k=1}^{p-1}k^3=\{\frac{(p-1)p}{2}\}^2$
$\sum_{m=1}^{25}x^{m}=\frac{x(1-x^{25})}{1-x}$

(4)　Σ記号と定数倍，和差

(a1 + b1)+ (a2 + b2)+ ···+ (an + bn)
= (a1 + a2 + ··· + an )+ (b1 + b2 + ···+ bn)

だから
$\sum_{k=1}^n(a_k+ b_k)=\sum_{k=1}^na_k+ \sum_{k=1}^nb_k$
が成り立つ．
また
ka1+ ka2 + ···+ kan = k(a1 + a2 + ··· + an )

だから
$\sum_{j=1}^nka_j=k\sum_{j=1}^na_j$
が成り立つ．

例9

$\sum_{k=1}^n(k+ k^2)=\sum_{k=1}^nk+\sum_{k=1}^nk^2$
$=\frac{n(n+ 1)}{2}+\frac{n(n+ 1)(2n+ 1)}{6}$
$=\frac{3n(n+ 1)+n(n+ 1)(2n+ 1)}{6}$
$=\frac{n(n+ 1)(2n+ 4)}{6}=\frac{n(n+ 1)(n+ 2)}{3}$

$\sum_{k=1}^n 3k=3\sum_{k=1}^n k=3\frac{n(n+ 1)}{2}$

※　定数倍と和・差については「Σをはずせる」ということで，関数の積について，次の２式は等しくない．（商についても，Σと商の順序を入れ替えると等しくならない．）

$\sum_{k=1}^n(a_kb_k)\leftarrow\times\rightarrow\sum_{k=1}^na_k\cdot\sum_{k=1}^nb_k$

そこで，Σ記号の内部が積の形になっているときは，展開して和・差，定数倍の形にしてからΣ記号をはずすようにする：
$\sum_{k=1}^n(k+ 3)^2=\sum_{k=1}^n(k^2+ 6k+ 9)$
$=\sum_{k=1}^nk^2+ 6\sum_{k=1}^nk+\sum_{k=1}^n 9$
$=\frac{n(n+ 1)(2n+ 1)}{6}+ 6\frac{n(n+ 1)}{2}+ 9n$

■即答問題■
（※必ず「半角数字」「１バイト文字の数字」で書くこと）

(2)
　次の数列について，なるべく簡単な規則を見つけて一般項を求めよ．

(3)　次の和を求めよ．

○···メニューに戻る