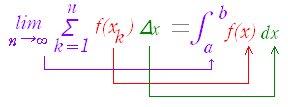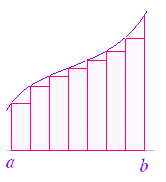
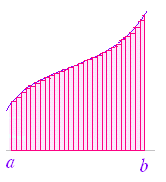
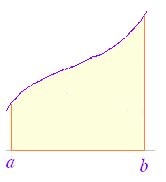
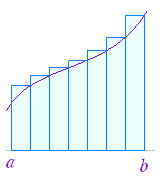
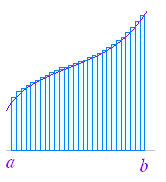
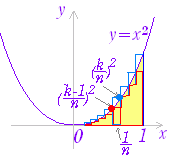
定積分と区分求積法

← PC版は別頁

== 定積分と区分求積法 == ○　はじめに

　この単元では，数列の和の極限値と定積分の関係について学ぶ．以下において，曲線 y=f(x)のグラフがx軸よりも上にあり，かつ，単調増加関数であるものについて説明するが，結果はこの条件にかかわらず成立することが分かっている．

(1)　不定積分と面積の関係

　高校数学II において定積分は，次のように導入した．
　区間 a≦x≦bにおいて曲線 y=f(x)のグラフがx軸よりも上にあるとき，図1のような図形の面積をSとおくとき，Sの（区間の右端の座標に x 関する）微分が縦の長さ f(x)となることを用いて，微分の逆計算としての不定積分

$S=\int f(x)dx$

から定数項を定めて，

$\int_a^b f(x)dx$

を定義した．

図1

(2)　区分求積法
　曲線で囲まれた図形の面積は，以下に述べる「区分求積法」の考え方によって求めることができる．

(*)　数列の和の極限⇔定積分
　以上の２つの方法で求めた結果は等しいので，数列の和の極限を定積分に直して計算したり，不定積分の関数形が分からない定積分の近似値を数値積分として求めることができる．

○　区分求積法における面積の定義

　上の図1のような図形を，長方形によって埋め尽くすことは難しいが，次の図2のように求める図形よりも少し小さな長方形の組（以下「下組」とする）と少し大きな長方形の組（以下「上組」とする）で囲むことはできる．
　区間 a≦x≦bを n等分したときにできる n個の長方形の面積の和を各々の面積とするとき，求める図形の面積Sは下組の面積Rと上組の面積T の間にある：
R≦S≦T 　区間 a≦x≦bを等分する nの値を限りなく大きくするとき（長方形の横幅を限りなく0に近づけるとき），
R=T
となることが知られており，この極限値を面積Sの定義とする．

図2

の和が限りなく0に近づく
$\Rightarrow$

≦S=

≦T=

の和が限りなく0に近づく
$\Rightarrow$

　この図形において，個々の面積は次のように作られる．
区間 a≦x≦bをn等分するので，各々の長方形の横幅をΔxとおくと，

Δx=

　n等分する点のx座標を左から順に，a=x₀，x₁，x₂，…，x_n=bとおくと，

x_k=a+kΔx

　長方形の面積はf(x_k)Δx

(1)
　下組は，各々の長方形の左端のx座標に対応する縦の長さを用いているから，

$R=\sum_{k=0}^{n-1}f(x_k)\Delta x$
$\lim_{n\rightarrow\infty}R=\lim_{n\rightarrow\infty}\sum_{k=0}^{n-1}f(x_k)\Delta x$

(2)
　上組は，各々の長方形の右端のx座標に対応する縦の長さを用いているから，

$T=\sum_{k=1}^{n}f(x_k)\Delta x$
$\lim_{n\rightarrow\infty}T=\lim_{n\rightarrow\infty}\sum_{k=1}^{n}f(x_k)\Delta x$

　これらが，等しいときこれを面積Sの定義とし，

$\int_{a}^{b}f(x)dx$

で表わす．すなわち

$\lim_{n\rightarrow\infty}\sum_{k=0}^{n-1}f(x_k)\Delta x=\int_{a}^{b}f(x)dx$
$\lim_{n\rightarrow\infty}\sum_{k=1}^{n}f(x_k)\Delta x=\int_{a}^{b}f(x)dx$

※　以上の解説においては， y=f(x)が単調増加関数であると仮定したが，この条件は緩めることができる．すなわち，区間 a≦x≦bにおいて，y=f(x)の増減の変化が有限回であるときは，各増加または減少の区間毎に上記の方法で求めて結果を加えると考えればよい．
　よって，y=f(x)が単調増加関数であるという条件はなくても成り立つ．
　（区間 a≦x≦bにおいて増減が無限回変化するような関数の定積分はここでは扱わない．）

例
　区間 0≦x≦1において，曲線 y=x² のグラフとx軸とで囲まれる図形の面積

1)
　0=x₀，x₁，x₂，…，x_n=1をn等分すると，Δx=
2)
　x_k=
3)
　下組の面積は，
$0^2\cdot\frac{1}{n}+(\frac{1}{n})^2\cdot\frac{1}{n}+(\frac{2}{n})^2\cdot\frac{1}{n}+\cdots+(\frac{k}{n})^2\cdot\frac{1}{n}+\cdots+(\frac{n-1}{n})^2\cdot\frac{1}{n}$
$=\frac{1}{n^3}\left(0^2+ 1^2+ 2^2+\cdots+k^2+\cdots+(n-1)^2\right)$
$=\frac{1}{n^3}\cdot\frac{(n-1)n(2n-1)}{6}\rightarrow\frac{1}{3}\hspace{10}(n\rightarrow\infty)$
4)
　上組の面積は，
$(\frac{1}{n})^2\cdot\frac{1}{n}+(\frac{2}{n})^2\cdot\frac{1}{n}+\cdots+(\frac{k}{n})^2\cdot\frac{1}{n}+\cdots+(\frac{n}{n})^2\cdot\frac{1}{n}$
$=\frac{1}{n^3}\left(1^2+ 2^2+\cdots+k^2+\cdots+ n^2\right)$
$=\frac{1}{n^3}\cdot\frac{n(n+ 1)(2n+ 1)}{6}\rightarrow\frac{1}{3}\hspace{10}(n\rightarrow\infty)$

○　上組と下組の値が一致するから，面積は
○　定積分と数列の和の極限の関係としては，
$\lim_{n\rightarrow\infty}\sum_{k=0}^{n-1}(x_k^2)\Delta x=\int_{0}^{1}x^2dx$
$\lim_{n\rightarrow\infty}\sum_{k=1}^{n}(x_k^2)\Delta x=\int_{0}^{1}x^2dx$
の，いずれも成り立つ．

○　要約

　limΣ と ∫は次のように対応する．

　　　　　　（ただし，x0=a，xn=b，Δx=）
（ $\lim_{n\rightarrow\infty}\sum_{k=0}^{n-1}f(x_k)\Delta x=\int_{a}^{b}f(x)dx$ でも同じ．）

１つの長方形の面積は f(xn)Δx
階段図形の面積は　Σf(xn)Δx
無限に細かく分ければ limΣf(xn)Δx

例と答

次の極限値を定積分で表わし，その値を求めよ．

(1)
$\lim_{n\rightarrow\infty}\sum_{k=1}^{n}\frac{1}{n+ k}$

$\frac{1}{n+ k}=\frac{1}{1+\frac{k}{n}}\cdot\frac{1}{n}$
xk=とおくと

$\frac{1}{1+\frac{k}{n}}\cdot\frac{1}{n}=\frac{1}{1+ x_k}\cdot\frac{1}{n}$
$f(x_k)=\frac{1}{1+ x_k}\Leftrightarrow f(x)=\frac{1}{1+ x}$
a=x0=0， b=xn==1

このとき，=でよい．

（原式）
$=\lim_{n\rightarrow\infty}\sum_{k=1}^{n}\frac{1}{n+ k}=\lim_{n\rightarrow\infty}\sum_{k=1}^{n}\frac{1}{1+\frac{k}{n}}\cdot\frac{1}{n}$
$=\lim_{n\rightarrow\infty}\sum_{k=1}^{n}\frac{1}{1+ x_k}\cdot\Delta x$
$=\int_0^1\frac{1}{1+ x}dx=\Bigl[\log(1+ x)\Bigr]_0^1=\log 2$

（要点）
Δx ⇔ dxに対応するものがないときは作る．

でくくる．

(2)
$\lim_{n\rightarrow\infty}\sum_{k=0}^{n-1}\frac{\pi}{n}\sin\frac{k\pi}{n}$

（ア）区間の幅を1とする考え方
$\lim_{n\rightarrow\infty}\sum_{k=0}^{n-1}\pi\sin\frac{k\pi}{n}\cdot\frac{1}{n}$ と変形する．
xk=とおくと πsin(π) = πsin(πxk)

f(xk)=πsin(π)⇔ f(x)=πsin(πx)

a=x0=0， b=xn==1

このとき，=でよい．

（原式） $=\int_0^1\pi\sin(\pi x)dx$
$=\Bigl[-\cos(\pi x)\Bigr]_0^1=-\cos \pi+ \cos 0=2$

（イ）区間の幅をπとする考え方
$\lim_{n\rightarrow\infty}\sum_{k=0}^{n-1}\sin\frac{k\pi}{n}\cdot\frac{\pi}{n}$ と変形する．
Δx=, xk=a+kΔx=とおくと

a=x0=0, b=xn=π

sin(π)=sin(xk)

f(xk)=sin(xk)⇔ f(x)=sin x

このとき，=でよい．

（原式） $=\int_0^{\pi}\sin xdx$
$=\Bigl[-\cos x\Bigr]_0^{\pi}=-\cos \pi+ \cos 0=2$

(3)
$\lim_{n\rightarrow\infty}\sum_{k=1}^{n}\frac{1}{\sqrt{n}}\cdot\frac{1}{\sqrt{n+ k}}$

$\lim_{n\rightarrow\infty}\sum_{k=1}^{n}\frac{1}{\sqrt{1+\frac{k}{n}}}\cdot\frac{1}{n}$
と変形する．
xk=とおくと =

f(xk)=⇔ f(x)=

a=x0=0， b=xn==1

このとき，=でよい．

（原式） $=\int_0^{1}\frac{1}{\sqrt{1+ x}}dx=\int_0^{1}(1+ x)^{-\frac{1}{2}}dx$
$=\Bigl[2(1+ x)^{\frac{1}{2}}\Bigr]_0^1=2\sqrt{2}-2$

（要点）
Δx ⇔ dxに対応するものがないときは作る．
でくくる．(ではない．←幅が変わる)

短答問題　　（･･･計算用紙：必要）

次の極限値を定積分で表わし，その値を求めよ．
（半角数字で入力）
(1)

=

xk=，Δx=とおくと = Δx

f(xk)=， f(x)=

a=x0=0， b=xn==1　このとき，=でよい．

(原式) $=\int_0^{1}\frac{x}{1+ x^2}dx=\frac{1}{2}\int_0^{1}\frac{2x}{1+ x^2}dx$
$=\frac{1}{2}\int_0^{1}\frac{(1+ x^2)\apos}{1+ x^2}dx=\frac{1}{2}\Bigl[\log(1+ x^2)\Bigr]_0^1=\frac{\log 2}{2}$

(2)

=(1+)2

xk=，Δx=とおくと (1+)2 = (1+xk)2Δx

f(xk)=(1+xk)2， f(x)=(1+x)2

a=x0=0， b=xn==1　このとき，=でよい．

(原式) $=\int_0^{1}(1+ x)^2dx=\Bigl[\frac{(1+ x)^3}{3}\Bigr]_0^1$
$=\frac{8}{3}-\frac{1}{3}=\frac{7}{3}$

(3)

xk=，Δx=とおく

f(xk)=cosxk， f(x)=cosx

a=x0=0， b=xn==　このとき，=でよい．

(原式) $=\int_0^{\frac{\pi}{2}}\cos xdx=\Bigl[\sin x\Bigr]_0^{\frac{\pi}{2}}=1$

○　数値積分

　不定積分が初等的に（既知の関数で）は求められない関数についても区分求積法の応用として，定積分を数値として求めることができる．

　区分求積法における面積
$\int_a^{b}f(x)dx=\lim_{n\rightarrow\infty}\sum_{k=0}^{n-1}f(x_k)\Delta x$
または $\lim_{n\rightarrow\infty}\sum_{k=1}^{n}f(x_k)\Delta x$
はn→ ∞ のとき真の値を表わすが，
$\sum_{k=0}^{n-1}f(x_k)\Delta x$ または $\sum_{k=1}^{n}f(x_k)\Delta x$
において，nに有限の十分大きな値を指定すると近似値となる．

　これらは，横幅Δxの区間 xk≦x≦xk+1において，f(x)の値を１つの定数で代用したものなので，面積の0次の近似となっている．
　これは，f(x)=a₀+a₁x+a₂x²+a₃x³+···のa₀のみを使うことに対応している．

　図3のように区間 0≦x≦1をn等分した場合，上または下にできる余りまたは不足となる三角形の
１辺の長さはだから，面積は()2に比例し，これがn個あるから，全体で誤差はのオーダーとなる．

　いくつかの曲線について，区間 0≦x≦1で調べてみると，10等分で小数第１位まで，100等分で小数第2位あたりまで正しいことが分かる．

図3

　台形公式
　図4のように，横幅Δxの区間 xk≦x≦xk+1の面積を台形に置き換えると，同じn等分でも，真の値にさらに近いものが得られる．これを台形公式という．
　台形の面積は，f(x_k)を上底，f(x_k+1)を下底，Δxを高さと考えると，

ΔS=

となるから，f(x_k)と f(x_k+1)の平均を高さに選んだことになる．

　台形公式は，f(x)=a₀+a₁x+a₂x²+a₃x³+···として，区間 xk≦x≦xk+1の両端が関数 f(x) と一致するように係数a₀，a₁を決めたことに対応しているので，面積の１次の近似となっている．

図4

※　シンプソンの公式

　区間 xk≦x≦xk+1の両端と中央の３点を通る２次関数で近似するものをシンプソンの公式という．これを用いると，近似の精度はさらによくなる．（２次の近似となる．）

例1

　標準正規分布を表わす確率密度関数
$f(x)=\frac{e^{-\frac{x^2}{2}}}{\sqrt{2\pi}}$
の不定積分は，初等的に表わせない．この関数について，
$\int_0^1f(x)dx$
をExcelを用いて台形公式で求めてみよう．

（解説）
100分割の台形公式で近似値を求める．
右図5のように
(1)　Ａ列にx座標を準備する．(編集→フィル→連続データの作成　など)
(2)　Ｂ列に=EXP(-A3*A3/2)/SQRT(2*PI())　などの計算式を書く．
(3)　Ｃ列に=(B3+B4)/2の計算式を書く．
(4)　Δxを各々掛けてから加えると一般には丸めの誤差が加算されるから，全部の和を求めてからΔx=0.01を掛ける．
Ｃ１に=SUM(C3:C102)*A4の計算式を書く．

===> 小数第4位までで，0.3413 となり実用に耐えうる数値となる．

図5

	A	B	C
1			0.34134273
2
3	0	0.39894228	0.398932307
4	0.01	0.398922334	0.398892417
5	0.02	0.3988625	0.398812648
6	0.03	0.398762797	0.398693025
7	0.04	0.398623254	0.398533584
8	0.05	0.398443914	0.398334372
･･･	･･･	･･･	･･･
102	0.99	0.244390351	0.243180538
103	1.00	0.241970725

　統計の教科書の巻末などにある正規分布表では小数第4位までで 0.3413 となっているが，ここで得られた結果はかなりよい近似となっており，0.34134273 となる．
　正規分布の確率を別途統計ソフトで計算したものは，0.34134474 となるので，小数第5位まで有効であることが分かる．

例2　　
$\int_0^{\varphi}\sqrt{1-k^2\sin^2x}dx\hspace{5}(0\lt k\lt 1)$
は第２種楕円積分と呼ばれ，不定積分は初等的に表せない．この関数について，
φ=，k=0.3の場合について，100分割の台形公式で近似してみよう．

（解説）
図6のように
(1)　Ａ列に0番からｋ番の番号を準備する．(編集→フィル→連続データの作成　など)
(2)　Ｂ1にの値を１つ書く．=PI()/2
Ｂ列にx座標を準備する：=A3*0.01*$B$1 などの計算式を書く．
(3)　Ｃ列に=SQRT(1-0.3*0.3*SIN(B3)*SIN(B3)) の計算式を書く．
(4)　Ｄ列に縦の長さの平均値を書く：=(C3+C4)/2
(5)　Ｄ１に=SUM(D3:D102)*B4の計算式を書く．

図6

	A	B	C	D
1		1.570796327		1.534833465
2
3	0	0	1	0.999994449
4	1	0.015707963	0.999988898	0.999972249
5	2	0.031415927	0.9999556	0.99992787
6	3	0.04712389	0.999900139	0.999861352
7	4	0.062831853	0.999822565	0.999772757
･･･	･･･	･･･	･･･	･･･
103	100	1.570796327	0.953939201

※　Visual Basic などのプログラミング言語を用いれば，指定した精度に達するまで分割数nを増やしていくことができる．（ただし，各々のプログラミング言語において変数の値には限界があることに注意：符号付の16bit整数 -32768〜32767 など）

短答問題

　Excelを用いて，100分割の台形公式により，次の定積分の値を求めよ．（解答は，小数第5位を四捨五入して小数第4位まで求めよ．）

(1)
$\int_0^{\frac{\pi}{2}}e^{^{\sin x}}dx$

解答チェック 　3.1044

(2)
$\int_0^{1}\sin(\frac{\pi}{2}x^2)dx$

解答チェック　0.4383

○･･･メニューに戻る