|
○ sinx の逆関数 三角関数のグラフ,例えば y=sinx のグラフは,右図1のように y=−1 からy=1 までの値を何度もとる. x の値を定めれば y の値は定まるが,ある y の値をとる元の x はただ一つではない.(x:多 対 y:1の対応) そこで,三角関数の逆の対応,すなわち y=sinx (−≦x≦) (−1≦y≦1)
を考え,y=sinx の逆関数を逆三角関数 y=arcsinx の値は, −〜 の値を考え,この値を「主値」と呼ぶ. このとき,y=arcsinx (−1≦x≦1) (−≦y≦ )となる. |
図1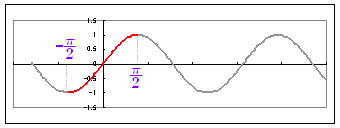 sin= ⇔ arcsin= sin=1 ⇔ arcsin1 = |
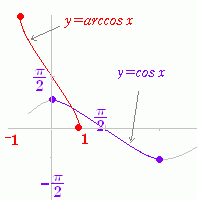
| ○ cosx の逆関数 y=cosx の逆関数は
すなわち, |
図2 cos= ⇔ arccos= cos=0 ⇔ arccos0 = |
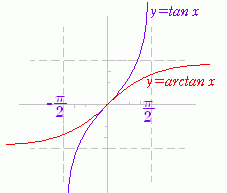
| ○ tanx の逆関数 y=tanx の逆関数は
すなわち, |
図3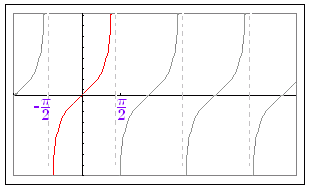 tan=1 ⇔ arctan1= tan0=0 ⇔ arctan0 = 0 |
| ■即答問題■ 次の値を求めよ. はじめに,左から問題を選び,続いて右から解答を選べ. ただし,主値は次の範囲にある値とする. |
0
|