９　正則行列と逆行列

９　正則行列と逆行列

　実数aについては，a≠0のとき，その逆数a−1が存在して，a·a−1=1が成り立つ．この節では，これと同様に，行列 $A$ について， $A$ $A$ −1=E( 単位行列 ) となる逆行列A−1が存在するための条件やその求め方を調べる．

○　n次正方行列 $A$ について $A$ $B$ = $B$ $A$ = $E_n$ を満たす行列 $B$ を $A$ の逆行列(inverse matrix) といいA−1で表わす．すべての行列が逆行列をもつわけではない．逆行列をもつ行列は正則(regular)であるという．

$A$

逆行列

$A^{-1}$

$A$

$A^{-1}$

$A$

$E_n$

$A$

$B$

$E_n$

$B$

$A$

$E_n$

$A$

$B$

$E_n$

$B$

$A^{-1}$

正則行列 $A$ の逆行列はただ１つである．

（証明）
行列 $B$ ， $C$ が $A$ の逆行列であると仮定すると，
( $A$ $B$ = ) $B$ $A$ = $E_n$ 　… (*1)
$A$ $C$ =( $C$ $A$ )= $E_n$ 　… (*2) (*1) 式の各辺に右から $C$ を掛けると， $B$ $A$ $C$ = $C$ (*2) 式により $A$ $C$ = $E_n$ だから $B$ = $C$

基本行列は正則である．

（証明）
$P=\begin{pmatrix}1&\cdots& 0&\cdots& 0\\ \vdots&&\vdots&&\vdots\\0& \cdots& c&\cdots& 0\\ \vdots & & \vdots & & \vdots\\0& \cdots& 0&\cdots& 1\end{pmatrix}$ (c≠0) については，
$\begin{pmatrix}1&\cdots& 0&\cdots& 0\\ \vdots&&\vdots&&\vdots\\0& \cdots& c&\cdots& 0\\ \vdots & & \vdots & & \vdots\\0& \cdots& 0&\cdots& 1\end{pmatrix}$ $\begin{pmatrix}1&\cdots& 0&\cdots& 0\\ \vdots&&\vdots&&\vdots\\0& \cdots&\frac{1}{c}&\cdots& 0\\ \vdots & & \vdots & & \vdots\\0& \cdots& 0&\cdots& 1\end{pmatrix}=E_n$
$\begin{pmatrix}1&\cdots& 0&\cdots& 0\\ \vdots&&\vdots&&\vdots\\0& \cdots&\frac{1}{c}&\cdots& 0\\ \vdots & & \vdots & & \vdots\\0& \cdots& 0&\cdots& 1\end{pmatrix}$ $\begin{pmatrix}1&\cdots& 0&\cdots& 0\\ \vdots&&\vdots&&\vdots\\0& \cdots& c&\cdots& 0\\ \vdots & & \vdots & & \vdots\\0& \cdots& 0&\cdots& 1\end{pmatrix}=E_n$
が成り立ち，逆行列
$P^{-1}=\begin{pmatrix}1&\cdots& 0&\cdots& 0\\ \vdots&&\vdots&&\vdots\\0& \cdots&\frac{1}{c}&\cdots& 0\\ \vdots & & \vdots & & \vdots\\0& \cdots& 0&\cdots& 1\end{pmatrix}$
が存在するから，Pは正則である．■

$Q=$ $\Bigl($

1	0	…	…	…	…	0
0	1	0	…	…	…	0
:		1				0
:			0	1		0
:			1	0		0
0					1	0
0	0	…	…	…	…	1

$\Bigr)$ ← i行
← j行

については　Qを左から掛けると，相手の行列の第i行と第j行が入れ替わるので，QQにより，Qの第i行と第j行が入れ替わり $E_n$ となる．
　つまり，QQ= $E_n$ だから，Q−1=Qとなり，逆行列が存在する（Q自身）から，Qは正則である．■

$R=$ $\Bigl($

1	0	…	…	…	…	0
0	1	0	…	c	…	0
:		1				0
:			1			0
:				1		0
0					1	0
0	0	…	…	…	…	1

$\Bigr)$ ←i行 ↑j列

については，Rを左から掛けると，相手の行列の第i行に第j行のc倍を加えるから，たとえば，
$\Bigl($

1	0	2	0
0	1	0	0
0	0	1	0
0	0	0	1

$\Bigr)$ $\Bigl($

1	0	−2	0
0	1	0	0
0	0	1	0
0	0	0	1

$\Bigr)$ $=E_4$

$\Bigl($

1	0	−2	0
0	1	0	0
0	0	1	0
0	0	0	1

$\Bigr)$ $\Bigl($

1	0	2	0
0	1	0	0
0	0	1	0
0	0	0	1

$\Bigr)$ $=E_4$
のように第 (i,j) 成分の符号を逆にすれば逆行列となる．よって，Rは正則である．■

定理４　次の(i)〜(v)は，それぞれ，n次正方行列 $A$ が正則であるための必要十分条件である．

$A\vec{x}=\vec{0}$

$\vec{b}$

$A\vec{x}=\vec{b}$

$A$

$E_n$

$A$

(証明)
　次の流れに沿って証明する．

(i)⇔(iv)の証明：
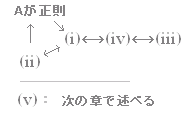
3.3節の定理３
　　　「同次方程式が自明解のみをもつ」ための必要十分条件は「rank( $A$ )=n」
によって示されている．　

(iv)⇔(iii)の証明：
rank ( $A$ ) =n，すなわちn次正方行列で異なる基本ベクトルがn個あること（既約な階段行列で先頭の1がｎ個あること）は， $A$ の基本形が $E_n$ であるということである．

正則→(i)の証明：
$A$ が正則ならば，その逆行列 $A^{-1}$ が存在するから， $A$ $\vec{x}$ = $\vec{0}$ 　 →　 $A^{-1}$ $A$ $\vec{x}$ = $A^{-1}$ $\vec{0}$ 　 →　 $\vec{x}$ = $\vec{0}$ となる．
（正則→(ii)も同様にして示される。すなわち， $A$ $\vec{x}$ = $\vec{b}$ かつ $A^{-1}$ の存在 → $A^{-1}$ $A$ $\vec{x}$ = $A^{-1}$ $\vec{b}$ → $\vec{x}$ = $A^{-1}$ $\vec{b}$ ）

(i)→(ii)の証明：
$A$ $\vec{x}$ 1= $\vec{b}$ ， $A$ $\vec{x}$ 2= $\vec{b}$ が成り立つとすれば，辺々引いて $A$ ( $\vec{x}$ 1− $\vec{x}$ 2) = $\vec{0}$
ここで (i) が成り立てば， $\vec{x}$ 1− $\vec{x}$ 2= $\vec{0}$ 　となるから， $\vec{x}$ 1= $\vec{x}$ 2が言える．すなわち (ii) が成立する．

(ii)→(i)の証明：
自明解 $\vec{x}$ = $\vec{0}$ 　は $A$ $\vec{x}$ = $\vec{0}$ 　の解だから， $A$ $\vec{x}$ = $\vec{0}$ がただ１つの解をもつならば，自明解のみが解となるのは明らかである．

(ii)→正則の証明：
　基本ベクトル $\vec{e}$ i( i = 1, 2, …, n )　に対して， $A$ $\vec{x}$ = $\vec{e}$ i　の解を $\vec{c}$ iとすると，
$A$ $\vec{c}$ 1= $\vec{e}$ i
$A$ $\vec{c}$ 2= $\vec{e}$ 2
…
$A$ $\vec{c}$ n= $\vec{e}$ n 列ベクトルを束ねて書くと， $A$ [ $\vec{c}$ 1 $\vec{c}$ 2… $\vec{c}$ n] = [ $\vec{e}$ 1 $\vec{e}$ 2… $\vec{e}$ n] = $E_n$
ここで， $C$ = [ $\vec{c}$ 1 $\vec{c}$ 2… $\vec{c}$ n] とおくと， $A$ $C$ = $E_n$ 　… (1) 　さらに，(ii)→(iii)だから $A$ の行基本変形により $E_n$ が得られる．
様々な種類の基本行列 $P$ ， $Q$ ， $R$ を変形の順に $H$ 1， $H$ 2，…， $H$ kで表わすと，
$H$ k… $H$ 2 $H$ 1 $A$ = $E_n$ が成り立つから， $D$ = $H$ k… $H$ 2 $H$ 1とおくと
$D$ $A$ = $E_n$ 　… (2) (1)(2) より， $D$ = $D$ $E_n$ = $D$ ( $A$ $C$ ) = ( $D$ $A$ ) $C$ = $E_n$ $C$ = $C$
よって， $A$ $C$ = $C$ $A$ = $E_n$ となるから， $A$ は正則で， $C$ = $D$ = $A^{-1}$ となる．

n次正則行列 $A$ , $B$ について，次が成り立つ.
(1)　 $A$ の逆行列はただ１つである．
(2)　逆行列 $A^{-1}$ も正則であり，( $A^{-1}$ )−1= $A$
(3)　転置行列t $A$ も正則であり，(t $A$ )−1=t( $A$ −1)
(4)　( $AB$ )−1= $B$ −1 $A$ −1

証明
(1)　２つ存在すると仮定して等しいことを示す．
(2)　逆行列の定義に当てはめる：「　 $A$ $B$ = $B$ $A$ = $E_n$ 　を満たす行列 $B$ を $A$ の逆行列といい $A^{-1}$ で表わす．」から，
$A^{-1}$ $A$ = $A$ $A^{-1}$ = $E_n$ 　により $A^{-1}$ の逆行列 ( $A^{-1}$ )−1が存在し， ( $A^{-1}$ )−1= $A$
(3)　2.2節において，転置行列について次の性質を示した：t(t $A$ ) = $A$ ，t( $A$ $B$ ) =t $B$ t $A$
t $A$ t( $A$ −1) =t( $A$ −1 $A$ ) =t $E_n$ = $E_n$
t( $A$ −1)t $A$ =t( $A$ $A$ −1) =t $E_n$ = $E_n$ となるから，(t $A$ )−1=t( $A$ −1)
(4)　 ( $AB$ )( $B$ −1 $A$ −1) = $A$ ( $B$ $B$ −1) $A$ −1= $A$ ( $E_n$ ) $A$ −1= $A$ $A$ −1= $E_n$
( $B$ −1 $A$ −1)( $AB$ ) = $B$ −1( $A$ −1 $A$ ) $B$ = $B$ −1( $E_n$ ) $B$ = $B$ −1 $B$ = $E_n$ だから，( $AB$ )−1= $B$ −1 $A$ −1

○　逆行列の求め方

$A$

$H$

$H$ k… $H$ 2 $H$ 1 $A$ = $E_n$

$H$ k… $H$ 2 $H$ 1= $A$ −1

$A$

$E_n$

行

$H$ k… $H$ 2 $H$ 1[ $A$		$E_n$ ]
↓		↓
[ $E_n$		$H$ k… $H$ 2 $H$ 1]

$A$

$E_n$

$H$

$A$

−1

例１
$A=\begin{pmatrix}1& 3\\ 2& 5\end{pmatrix}$ の逆行列を求める．

2行+1行×(−2)

$A=\Bigl(\begin{matrix}1& 3\\ 2& 5\end{matrix}\hspace{3}\left|\hspace{3}\begin{matrix}1& 0\\ 0& 1\end{matrix}\Bigr)$ $\Rightarrow$ $\Bigl(\begin{matrix}1& 3\\ 0& -1\end{matrix}\hspace{3}\left|\hspace{3}\begin{matrix}1& 0\\ -2& 1\end{matrix}\Bigr)$

2行×(−1)

$\Rightarrow$ $\Bigl(\begin{matrix}1& 3\\ 0& 1\end{matrix}\hspace{3}\left|\hspace{3}\begin{matrix}1& 0\\ 2& -1\end{matrix}\Bigr)$

1行+2行×(−3)

$\Rightarrow$ $\Bigl(\begin{matrix}1& 0\\ 0& 1\end{matrix}\hspace{3}\left|\hspace{3}\begin{matrix}-5& 3\\ 2& -1\end{matrix}\Bigr)$

ゆえに， $A^{-1}=\begin{pmatrix}-5& 3\\ 2& -1\end{pmatrix}$

例２

$A=\begin{pmatrix}0& 1& 2\\ 1& 1& 1\\ 2& 1& 1\end{pmatrix}$ の逆行列を求める．

1行と2行の入れ替え

$A=$ $\Biggl($ $\begin{matrix}0& 1& 2\\ 1& 1& 1\\ 2& 1& 1\end{matrix}\hspace{3}\left|\hspace{3}\begin{matrix}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{matrix}$ $\Biggr)$ $\Rightarrow$ $\Biggl($ $\begin{matrix} 1& 1& 1\\0& 1& 2\\ 2& 1& 1\end{matrix}\hspace{3}\left|\hspace{3}\begin{matrix} 0& 1& 0\\1& 0& 0\\ 0& 0& 1\end{matrix}$ $\Biggr)$

3行+1行×(−2)

$\Rightarrow$ $\Biggl($ $\begin{matrix} 1& 1& 1\\0& 1& 2\\ 0& -1& -1\end{matrix}\hspace{3}\left|\hspace{3}\begin{matrix} 0& 1& 0\\1& 0& 0\\ 0& -2& 1\end{matrix}$ $\Biggr)$

1行+2行×(−1), 3行+2行

$\Rightarrow$ $\Biggl($ $\begin{matrix} 1& 0& -1\\0& 1& 2\\ 0& 0& 1\end{matrix}\hspace{3}\left|\hspace{3}\begin{matrix} -1& 1& 0\\1& 0& 0\\ 1& -2& 1\end{matrix}$ $\Biggr)$

1行+3行, 2行+3行×(−2)

$\Rightarrow$ $\Biggl($ $\begin{matrix} 1& 0& 0\\0& 1& 0\\ 0& 0& 1\end{matrix}\hspace{3}\left|\hspace{3}\begin{matrix} 0& -1& 1\\-1& 4& -2\\ 1& -2& 1\end{matrix}$ $\Biggr)$

ゆえに $A^{-1}=\begin{pmatrix}0& -1& 1\\ -1& 4& -2\\ 1& -2& 1\end{pmatrix}$

■確認テスト■　　　次の空欄を埋めよ．

(1)　次の行列が正則行列かどうか判定せよ．

$\begin{pmatrix}0& 1& 2\\ 1& 0& 1\\ 2& 1& 0\end{pmatrix}$ …　[ 計算:見る|隠す]

原式→1行と２行の入れ替え

$\begin{pmatrix}1& 0& 1\\ 0& 1& 2\\ 2& 1& 0\end{pmatrix}$

→3行+1行×(−2)

$\begin{pmatrix}1& 0& 1\\ 0& 1& 2\\ 0& 1& -2\end{pmatrix}$

→3行+2行×(−1)

$\begin{pmatrix}1& 0& 1\\ 0& 1& 2\\ 0& 0& -4\end{pmatrix}$

→3行÷(−4)

$\begin{pmatrix}1& 0& 1\\ 0& 1& 2\\ 0& 0& 1\end{pmatrix}$

→1行+3行×(−1)

$\begin{pmatrix}1& 0& 0\\ 0& 1& 2\\ 0& 0& 1\end{pmatrix}$

→2行+3行×(−2)

$\begin{pmatrix}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{pmatrix}$

…行列が　次正方行列で，その階数が　だから，
（正則である　正則でない　）　

採点するやり直す

(2)　次の行列が正則行列かどうか判定せよ．

$\begin{pmatrix}3& 1& 2\\ 1& 1& 0\\ 2& 1& 1\end{pmatrix}$ 　…　[ 計算:見る|隠す]

原式→1行と２行の入れ替え

$\begin{pmatrix}1& 1& 0\\ 3& 1& 2\\ 2& 1& 1\end{pmatrix}$

→2行+1行×(−3)

$\begin{pmatrix}1& 1& 0\\ 0& -2& 2\\ 0& -1& 1\end{pmatrix}$

→2行÷(−2)

$\begin{pmatrix}1& 1& 0\\ 0& 1& -1\\ 0& -1& 1\end{pmatrix}$

→1行+2行×(−1)

$\begin{pmatrix}1& 0& 1\\ 0& 1& -1\\ 0& 0& 0\end{pmatrix}$

…行列が　次正方行列で，その階数が　だから，
（　正則である　正則でない　）　

採点するやり直す

(3)　次の行列の逆行列を求めよ．

$\begin{pmatrix}1& 1& 0\\ -2& 1& 2\\ 2& 3& 1\end{pmatrix}$ 　…　[ 計算:見る|隠す]

$\Biggl($ $\begin{matrix}1& 1& 0\\ -2& 1& 2\\ 2& 3& 1\end{matrix}\hspace{3}\left|\hspace{3}\begin{matrix}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{matrix}$ $\Biggr)$

→2行+1行×2,
3行+1行×(−2)

$\Rightarrow$ $\Biggl($ $\begin{matrix} 1& 1& 0\\0& 3& 2\\ 0& 1& 1\end{matrix}\hspace{3}\left|\hspace{3}\begin{matrix} 1& 0& 0\\2& 1& 0\\ -2& 0& 1\end{matrix}$ $\Biggr)$

→2行と3行の入れ替え

$\Rightarrow$ $\Biggl($ $\begin{matrix} 1& 1& 0\\ 0& 1& 1\\0& 3& 2\end{matrix}\hspace{3}\left|\hspace{3}\begin{matrix} 1& 0& 0\\ -2& 0& 1\\2& 1& 0\end{matrix}$ $\Biggr)$

→1行+2行×(−1),
3行+2行×(−3)

$\Rightarrow$ $\Biggl($ $\begin{matrix} 1& 0& -1\\ 0& 1& 1\\0& 0& -1\end{matrix}\hspace{3}\left|\hspace{3}\begin{matrix} 3& 0& -1\\ -2& 0& 1\\8& 1& -3\end{matrix}$ $\Biggr)$

→3行×(−1)

$\Rightarrow$ $\Biggl($ $\begin{matrix} 1& 0& -1\\ 0& 1& 1\\0& 0& 1\end{matrix}\hspace{3}\left|\hspace{3}\begin{matrix} 3& 0& -1\\ -2& 0& 1\\-8& -1& 3\end{matrix}$ $\Biggr)$

→1行+3行, 2行+3行×(−1)

$\Rightarrow$ $\Biggl($ $\begin{matrix} 1& 0& 0\\ 0& 1& 0\\0& 0& 1\end{matrix}\hspace{3}\left|\hspace{3}\begin{matrix} -5& -1& 2\\ 6& 1& -2\\-8& -1& 3\end{matrix}$ $\Biggr)$

$A^{-1}=$

$\Bigl($

$\Bigr)$

採点するやり直す

(4)　次の行列の逆行列を求めよ．

$\begin{pmatrix}1& 0& 0\\ 2& 1& 0\\ 3& 0& 1\end{pmatrix}$ …　[ 計算:見る|隠す]

$\Biggl($ $\begin{matrix}1& 0& 0\\ 2& 1& 0\\ 3& 0& 1\end{matrix}\hspace{3}\left|\hspace{3}\begin{matrix}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{matrix}$ $\Biggr)$

→2行+1行×(−2), 3行+1行×(−3)

$\Rightarrow$ $\Biggl($ $\begin{matrix} 1& 0& 0\\0& 1& 0\\ 0& 0& 1\end{matrix}\hspace{3}\left|\hspace{3}\begin{matrix} 1& 0& 0\\-2& 1& 0\\ -3& 0& 1\end{matrix}$ $\Biggr)$

$A^{-1}=$

$\Bigl($

$\Bigr)$

採点するやり直す

○･･･メニューに戻る