◇1変数での変数変換◇1変数の関数において,変数変換を行うことにより分かりやすい形に直すことはよく行われる.例1 y=4sin x−cos 2x の最大値,最小値を求めるとき, sin x=t とおくと,−1≦t≦1 y=4sin x−(1−2sin2x)=4t−(1−2t2)=2t2+4t−1 =2(t2+2t)−1=2(t+1)2−3 t=−1 (x=−+2nπ)のとき最小値−3 をとる. t= 1 (x=+2nπ)のとき最大値 5 をとる. |
| 例2 y=ex+e−x の最小値を求めるとき, ex=t とおくと,y=t+ ex=t>0 だから,相加平均と相乗平均の関係により, y=t+≧2 (等号はt=1 のとき) よって,x=0 (t=1)のとき,最小値 2 をとる. |
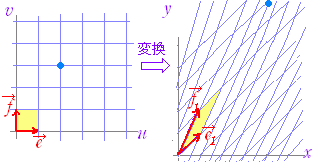
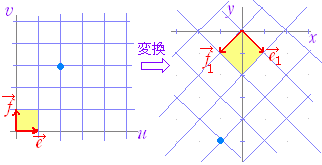
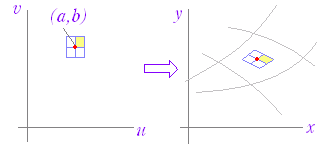
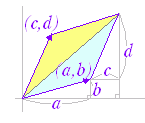
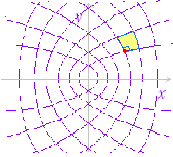
◇2変数での変数変換◇○ 以下においては,uv 平面上の点 (u , v) に対してxy 平面上の点 (x , y) を対応させる対応(変換)について考える.
○ 変換のうち,次の形で表わされる1次変換が特に重要である.
○ 1次変換は,行列を用いて次の形で表わすことができる. のとき,任意の点 (x , y) に対して,原像 (u , v) がただ1つ存在する. |
||||||
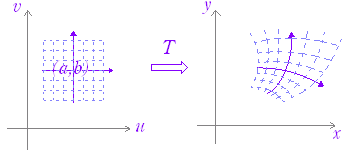 ※ 平面上の点 (u , v)∈R2 を平面上の点 (x , y)∈R2 に対応させる写像 T :R2→R2は変換と呼ばれる.(さらに,R2→R2の「1対1の写像」であることや「上への写像」であることを条件にすることもある.R2→R2の「上への1対1の写像」となっているときは,平面全体は平面全体に写され,ある点 (x , y) の原像 (u , v) はただ1つに定まる.) ※ 後に述べる(第7章)重積分での利用法に合わせて,以下においては, (u , v)→ (x , y) の形で変数の変換を考える. |