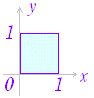
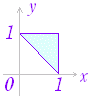
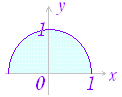
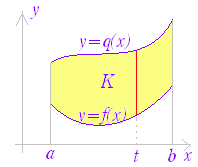
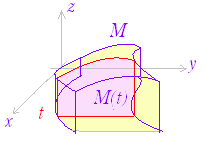
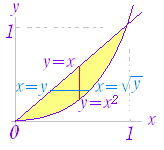◇累次積分◇区間 a≦x≦b において不等式 p(x)≦y≦q(x) を満たす xy 平面上の領域を K とする.K 上で定義される関数 z=f(x , y) ≧0 について,不等式 0≦z≦f(x , y) を満たす xyz 空間の領域(立体)を M とするとき,立体 M の体積を求めることを考える.集合記号で表わすと次の領域となっている:
K={(x,y)|a≦x≦b,p(x)≦y≦q(x)}
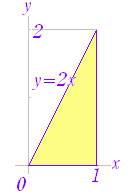
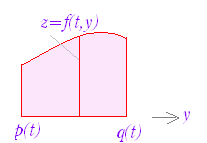
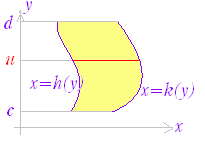
M={(x,y,z)|(x,y)∈K,0≦z≦f(x,y)} 図2,図3において桃色で示した x=t の断面の面積を M(t) とすると, ※ 上の説明では f(x , y) ≧0 の場合について,体積を求めたが,f(x , y) が必ずしも正または0とは限らないとき重積分は体積を表わさないが,累次積分で求められる事情は同じである. ※ 図4のように,領域 K の形によっては,y=u の断面から求める方が求めやすいことがある.この場合は, |
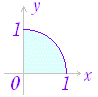
図1
    |