◇1変数関数の増減表◇※ このページでは,関数f(x)やf ’(x)が連続なものを扱う.したがって,f ’(x)の符号が変化するときは,必ずf ’(x)=0となる点が存在する. 1.[増加,減少の定義] ○ ある区間a≦x≦b内の任意の値x1, x2について,
○ ある区間a≦x≦b内の任意の値x1, x2について, |
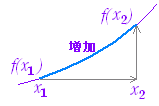  |
◇1変数関数の増減表◇※ このページでは,関数f(x)やf ’(x)が連続なものを扱う.したがって,f ’(x)の符号が変化するときは,必ずf ’(x)=0となる点が存在する. 1.[増加,減少の定義] ○ ある区間a≦x≦b内の任意の値x1, x2について,
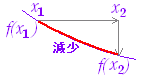
○ ある区間a≦x≦b内の任意の値x1, x2について, |
  |
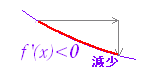
| 2.[導関数を用いた増減の判定] (単調)増加及び(単調)減少は,異なる2つの値x1, x2に対する関数の値を比較して得られる性質であるので,原理的には1点の値f(x)やf ’(x)のみによっては判断できないものであるが,1つの区間a≦x≦bにおいてf ’(x)が常に正であるならば,この区間で(単調)増加であることを示すことができる.(平均値の定理を用いて証明される.) 同様にして,1つの区間a≦x≦bにおいてf ’(x)が常に負であるならば,この区間で(単調)減少であることを示すことができる. ○ ある区間a≦x≦b内で
|
  |
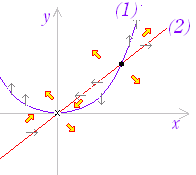
| 3.[極値の定義] ○ 関数f(x)についてx=aのまわりで,つねに 極大となるところx=aでは,関数f(x)が増加から減少に変化し, ○ 関数f(x)についてx=aのまわりで,つねに 極小となるところx=aでは,関数f(x)が減少から増加に変化し, ○ 極大値と極小値をまとめて極値という. ○ 極値→f ’(x)=0でかつf ’(x)の符号が変化する[右図1]
※ この章では増減表を用いた極値の調べ方を解説したが,後の章で増減表を用いない極値の調べ方にも触れる.(2変数関数についても同様) |
||||||||||||
極大の前後では,f ’(x)が正から負に変化してあり,極大のところではf ’(x)=0となる.
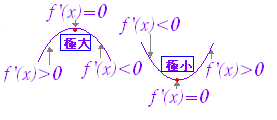 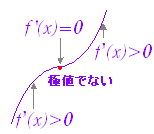 ※ 高校以来学んでいるように,極大・極小はその点のまわりだけの性質で,一定の区間で一番大きい,小さいを表わす最大・最小とは別のものである. 極大であっても,最大である場合も,最大でない場合もある. 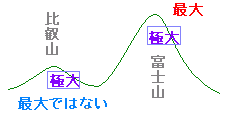 |
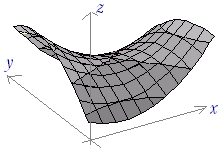
◇2変数関数の増減表◇1.[2変数関数の極値]○ 2変数関数f(x, y)について,点(a, b)のまわりで,つねに 極大となるところでは,=0 ,=0となり,各々増加から減少に変化する. ○ 2変数関数f(x, y)について,点(a, b)のまわりで,つねに 極小となるところでは,=0 ,=0となり,各々減少から増加に変化する. ○ 1変数関数のときと同様に,極大値と極小値をまとめて極値という. ※ 峠を越える道路は通常,右図5の青で示した経路となる.青で示した方向で x座標だけが変化するとすると,この道路は各yの最小値を取りながら山を越えるようになっている.特に鞍点(峠)では,y方向に見れば極小,x方向に見れば極大となるが,2変数関数としては極値でない.(これよりも大きいところも小さいところもある.) 右図6に示した点(一人掛けソファーの中心部)も=0, =0であるが極値ではない. |
図3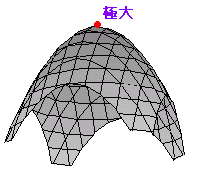 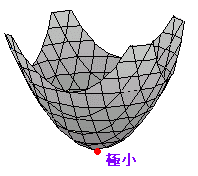 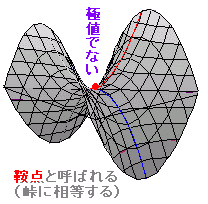 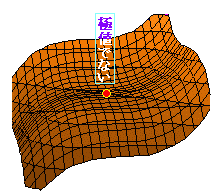 |
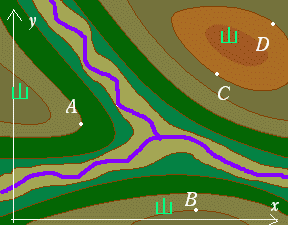
| 問題 右の等高線で,点B C, Dについてfx,fyの符号を埋めよ.(初めに
[選択肢] |
|||||||||||||||
 |
| 2.[2変数関数の増減表] 2変数関数で極値となるところでは,=0 ,=0が成り立つが,この連立方程式の解となる(x, y)が実際に極値となるかどうか[上記の図5,図6でなく図3,図4となるかどうか]は,右図のように2変数関数の増減表を作って調べる. (手順) (1)=0の曲線を描く (2)=0の曲線を描く 以上の(1)(2)はていねいに描く必要はない.実際には,これら2曲線の交点(a, b)(連立方程式の解)とその付近での(1)(2)の向きが分かればよい. (3)=0の曲線上での符号に応じてzが増える向きに矢印を描く(↑または↓) (4)=0の曲線上でも同様に右向き又は左向きの矢印を描く.(→または←) (5)4個の領域について,左で上なら左上向き45°の太めの矢印を描く.右下なら右下向き45°とする.以下同様.(これらは各点での傾き(,)を正確に反映している必要はなく,最終的に点(a, b)に向かっているか,離れているかが分かればよいので,おおまかに45°で描けばよい.) (6)4個の領域について矢印が描けたら,これらの矢印が全部点(a, b)に向かっていれば,(a, b)は極大値,全部点(a, b)から離れていけば,(a, b)は極小値とする.それ以外の場合は極値でない. ※ 次の関係に注意: 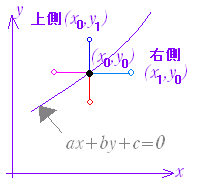 左の図でa>0のとき, 左の図でa>0のとき,x0<x1ならば, ax0+by0+c=0<ax1+by0+c 同様にb>0のとき, y0<y1ならば, ax0+by0+c=0<ax0+by1+c |
増減表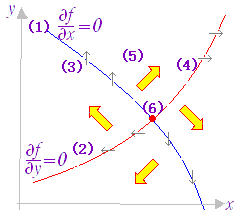 例1 z=f(x, y)=x2−2xy+3y2−4x+8yの極値を求めよ. (答案) 連立方程式 =2x−2y−4=0・・・(1) =−2x+6y+8=0・・・(2) を解くと,x=1 , y=−1 (1)よりも右にあれば(xが大きければ),>0となるから,(1)よりも右にある部分に(→)を入れる. ※この場合は,(1)よりも下にあれば(yが小さければ)>0となるといっても同じ. 逆に,(1)よりも左にあれば<0となるから,(1)よりも左にある部分に(←)を入れる.( (2)の上だけでよい. ) ※この場合は,(1)よりも上にあれば(yが大きければ)<0となるといっても同じ. ※※ (1)では=0が成り立つ.(1)以外ではは正か負かいずれかとなる.つまり,xが増えれば,zは増えるか減るかいずれかとなる.この符号は計算しやすい点の座標を代入して求めてもよい.例えば (0 , 0 )では<0だから(0 , 0 )を含む領域では←になる. (2)よりも上にあれば>0となるから,(2)よりも上にある部分に(↑)を入れる.逆に,(2)よりも下にあれば<0となるから,(2)よりも下にある部分に(↓)を入れる.( (1)の上だけでよい. ) ※で示した考え方は,上と同様. 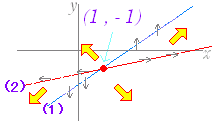 |
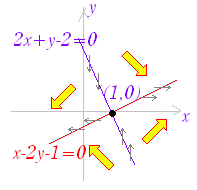
| 例2 z=f(x, y)=x2+xy−y2−2x−yの極値を調べよ. (答案) =2x+y−2=0・・・(1) = x−2y−1=0・・・(2) を解くと,x=1 , y=0 (1)よりも上では(yが大きければ)>0で右矢印 (1)よりも下では(yが小さければ)<0で左矢印 (2)よりも右では(xが大きければ)>0で上矢印 (2)よりも左では(xが小さければ)<0で下矢印 ※ 計算しやすい点の座標を代入する方法で行うと, (0 , 0)では2x+y−2<0, x−2y−1<0となるから, (1)は負,(2)も負:左下向き 次に(1)を横切ると左右の向きが変り,(2)を横切ると上下の向きが変ることに注意すると,全部の 増減表を作ると右図のようになるから,極値はない. |
  |
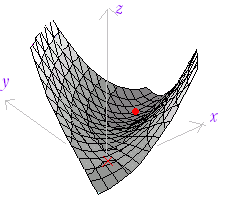
| 例3 z=f(x, y)=2x3−6xy+3y2の極値を調べよ. (答案) =6x2−6y=6(x2−y)=0・・・(1) =−6x+6y=−6(x−y)=0・・・(2) を解くと,(0 , 0) , (1 , 1) (1 , 0)において,→↓ 以下境界線を横切るたびに→↓の向きを入れ換えると右図の増減表ができる. (1 , 1)において極小値−1をとる. (0 , 0)では極値とはならない. |
  |
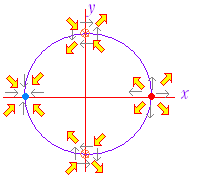
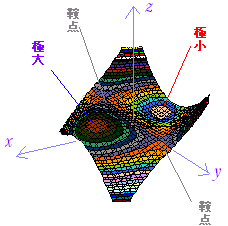
| 例4 z=f(x, y)=x3+3xy2−3xの極値を調べよ. (答案) =3x2+3y2−3=3(x2+y2−1)=0・・・(1) = 6xy=0・・・(2) を解くと,(1 , 0) , (0 , 1) , (−1 , 0) , (0 ,−1) (1 , 1)において,→↑ 以下境界線を横切るたびに→↓の向きを入れ換えると右図の増減表ができる. (1 , 0)において極小値−2をとる. (−1 , 0)において極大値2をとる. (0 , 1) , (0 ,−1)では極値とはならない. |
  |
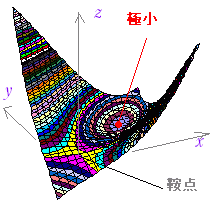
| 問題 1.次の関数の増減表を作れ.(右図で,初めに (1) z=f(x, y)=x3−3xy+y3 Help→途中計算鳥瞰図 =3x2−3y=3(x2−y)=0・・・(1) =−3x+3y2=−3(x−y2)=0・・・(2) を解くと,(0 , 0) , (1 , 1) (1 , 0)では→↓ |
||
 |
||
| (2) z=f(x, y)=2x3−6xy−12x+3y2 Help→途中計算鳥瞰図 =6x2−6y−12=6(x2−y−2))=0・・・(1) =−6x+6y=−6(x−y)=0・・・(2) を解くと,(−1 ,−1) , (2 , 2) (0 , 1)では←↑ |
||
 |
| 2.次の関数の極値を求めよ. 増減表は右図で,初めに 極値は,該当するものを選べ. Help→途中計算鳥瞰図 =4x−2y+2=2(2x−y+1)=0・・・(1) =−2x+2y+2=−2(x−y−1)=0・・・(2) を解くと,(−2 ,−3) (0 , 0)では→↑ |
||||
|
||||
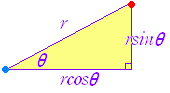
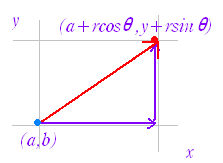
| 3.[方向微分] 右図のようにx軸の正の向きとなす角がθである斜辺に沿って長さrだけ進むと,x座標がrcosθ,y座標がrsinθだけ大きくなるから,点(a, b)からx軸の正の向きとなす角がθである斜辺に沿って長さrだけ進んだ点の座標は(x+rcosθ,y+rsinθ)となる. |
 |
| この方向に沿った平均変化率は となるが,これをx軸方向の増加とy軸方向の増加の2段に分けて求めると, =+ 微分係数は, = + ここで第1項は, · cosθ =· cosθ=cosθ 第2項は, =sinθ =sinθ =sinθ となるから,次の式を得る. cosθ+sinθ この式を,ベクトル=(cosθ,sinθ)方向の微分係数といい,で表わす.すなわち, =cosθ+sinθ
|
 各々の点(a, b)に対して ||
が最大となる角度θが定まり,この角度θに沿って下降(または上昇)すれば,最短距離で下降(または上昇)することができる. . 曲面にボールをそっと置くと,ボールは勾配ベクトルに沿って(逆向きに)転がっていくので,このボールを追跡すると2変数関数の極小値を求めることができる. 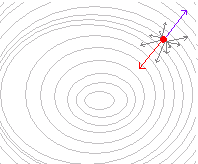 |
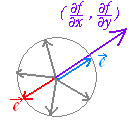
| 4.[勾配ベクトル] ○ 方向微分係数は,各点(a, b)ごとに定まるベクトル (,) と単位ベクトル=(cosθ,sinθ)の内積となっているから,が (,) と同じ向きのとき最大となる. grad f(a, b)=(,)
で定められるベクトルを勾配ベクトルという.勾配ベクトルは各点(a, b)において関数f(x, y)が最も効果的に増加する向きを表わしている.(勾配ベクトルの逆向きが最も効果的に減少する向きとなる.) ○ 第2章で述べた等高線に沿った接線の方程式
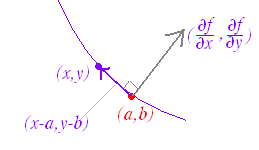
fx(a, b)(x−a)+fy(a, b)(y−b)=0
は,右図のように接線上の点P(x, y),接点A(a, b)に対してベクトル
=(x−a, y−b)と勾配ベクトル (,) が垂直であることを示している.すなわち,「勾配ベクトルは等高線に垂直である.」 |
  |
| ○ 勾配ベクトルに沿った移動の実演 (1) 次の実演1は,上の問題2.の z=f(x, y)=2x2−2xy+y2+2x+2yについて,初期値(0, 0)からr=0.1ずつ,勾配ベクトルの逆向きに進んだときのシミュレーションで,「試行回数が50回になるか又は勾配ベクトルの大きさが 0.01以下」になれば止まるプログラムである.上記の結果と比較してみよ. (2) 実演2は,上と同じ2変数関数について,初期値を(−3, 0)にしたものである. |