微分について

◇１変数関数の微分◇

１．　微分係数と導関数

　微分とは，「微かかすかに分かる」ことではなく，「微小に分ける」ことをいう．

［記号と用語］
○
　xがaからbまで変化するとき，関数y=f(x)の値はf(a)からf(b)まで変化する．このときxの増分Δx=b−aに対するyの増分Δy=f(b)−f(a)の比を，xがaからbまで変化するときの関数y=f(x)の平均変化率という．

平均変化率： $\frac{f(b)-f(a)}{b-a}$

○
　上のように定義される平均変化率において，bを限りなくaに近づけたときの極限を，x=aにおける関数f(x)の微分係数といい，f ’(a)で表わす．

微分係数： $f\apos(a)=\lim_{b\rightarrow a}\frac{f(b)-f(a)}{b-a}$

○　aが決まれば，その点における微分係数f’(a)が定まる．aを変数とすれば，この対応は１つの関数となり，関数f(x)から導かれた関数として，f(x)の導関数と呼ばれ，f’(x)で表わされる．

導関数： $f\apos(x)=\lim_{b\rightarrow x}\frac{f(b)-f(x)}{b-x}$

○　関数f(x)の導関数f ’(x)はf(x)の微分ともいう．また，関数f(x)から導関数f ’(x)を求めることを微分するという．

※平均変化率は，a，bの代わりに，aとxの増分h(=b−a)を用いて，次の形に書くこともできる．この定義の方が計算・変形が簡単になることが多い．

平均変化率： $\frac{f(a+ h)-f(a)}{h}$

微分係数，導関数は各々次の形になる．

微分係数： $f\apos(a)=\lim_{h\rightarrow 0}\frac{f(a+ h)-f(a)}{h}$

導関数： $f\apos(x)=\lim_{h\rightarrow 0}\frac{f(x+ h)-f(x)}{h}$

　平均変化率は，２点A(a , f(a) )，B(b , f(b) )を結ぶ線分ABの傾きを表わしている．

　微分係数は，点A(a , f(a) )における接線の傾きを表わしている．
　※　「微分できる」とは，「接線が引ける」ことであるといえる．

　y=f(x)の導関数を表わすために，次のような記号が使われる．

$y\apos\hspace{20}f\apos(x)\hspace{20}\frac{dy}{dx}\hspace{20}\frac{d}{dx}f(x)\hspace{20}\frac{df}{dx}\hspace{20}f\apos$

　x=aにおける微分係数を表わすためには，次のような記号が使われる．

$f\apos(a)\hspace{20}y\apos|_{x=a}\hspace{20}(\frac{dy}{dx})_a\hspace{20}(\frac{dy}{dx})_{x=a}\hspace{20}(y\apos)_a$

※　社会生活においては関数の値f(x)よりも，その変化率（微分）f ’(x)の方に関心があることも多い．

　例えば，「景気がよくなった」という場合，企業収入や個人所得の現在高が幾らであるかには関係なく，それらが増えているかどうかに関心が向いている．
　また，「今日は暖かくなった」という場合，その日の温度だけを言っているのでなく，前の数日との比較して温度が高いかどうかを言っていることが多い．
　海や湖での釣果は，水温が18度だったらどうかというよりは，17度から18度に上がったら釣れるが，19度から18度に下がったら釣れないというように増加傾向かどうかに左右されることがある．

２．　微分係数と導関数の例

例1
$f(x)=x^2$ のとき
(1)
$f\apos(a)=\lim_{h\rightarrow 0}\frac{(a+ h)^2-a^2}{h}$
$=\lim_{h\rightarrow 0}\frac{2ah+ h^2}{h}=\lim_{h\rightarrow 0}(2a+ h)=2a$

(2)　 $f\apos(3)=6$ 　　 (3)　 $f\apos(x)=2x$

多項式で表わされる関数については，次が成り立つ．
・　f(x)=k（kは定数）　→　f ’(x)=0
・　f(x)=xn（nは正の整数）　→　f ’(x)=nxn−1

３．　2次導関数（２階導関数）

（小話）
　ガリレイやニュートンなどの物理学における先人達のおかげで，今日では誰でも「慣性の法則」（力を受けていない物体は，止まるのではなく同じ速さで運動し続けるということ）を知っている．

　エジプトやギリシャの時代においても，力と速さの関係など自然法則には深く注意が払われていたが，力の大きさによって速度vが決まるのでなく加速度aが決まるという関係はなかなか発見されなかった．

　これは，馬車を引くような日常の作業では，空気や車輪の抵抗が大きく，ただちに終速度が力に比例してしまうという日常体験の影響が大きいと考えられている．

　すなわち，力学の方程式 (質量)×a=（力）−（抵抗係数）×v･･･(1) において，加速度aは右辺：「力から抵抗を引いたもの」に比例するのであるが，速度が増すと抵抗が大きくなるため，すぐに加速度 aが0に近づき，力が終速度に比例する
（力）=（抵抗係数）×v･･･(2) という関係が見えていたことになる．（　(1)が意識されずに(2)が意識された．）

　真空中などで抵抗のない世界では，
(質量)×a=（力）･･･(3) 加速度は力に比例するという運動の法則が成り立つ．

○　運動の法則では，力は，加速度＝速度の変化率＝座標の第2次導関数と関係している．

○　さらに，エコで過ごすには第3次導関数を小さくするのがよいということもできる．
　すなわち，人間の活動においても，力の入れ方をしばしば変えなければならないような生活は疲労が激しい．長距離を走るときは力のむらが少ないように，「加速度の変化」を小さくして走るのがよく，自動車では急発進や急ブレーキをなくせば燃料の節約となる．
　「加速度の変化率」は躍度と呼ばれ座標の第3次導関数となる．

　物体の座標（簡単のためにx座標のみで考える）をxとするとき，単位時間（例えば秒）当りの座標の変化の割合が速度vである．すなわち，座標xを時間tで微分すると速度になる．

　さらに，速度vの単位時間当りの変化の割合が加速度aである．すなわち，速度vを時間tで微分したものが加速度aになる．座標xから言えば，座標xを時間tで2階（回）微分したものが加速度aとなる．

関数y=f(x)の第2次導関数（2階導関数）は
$y\apos\apos\hspace{20}f\apos\apos(x)\hspace{20}\frac{d^2y}{dx^2}\hspace{20}\frac{d^f}{dx^2}$ で表わされる．

例
・　f(x)=xn→　f ’(x)=nxn−1→　f ”(x)=n(n−1)xn−2
・　f(x)=sin x→　f ’(x)=cos x→　f ”(x)=−sin x

４．　近似式

　微分係数 $f\apos(a)=\lim_{h\rightarrow 0}\frac{f(a+ h)-f(a)}{h}$
は極限で定義されているが，hが0に十分近い値のときは，右辺の分数は微分係数の近似値となる．すなわち，

$f\apos(a)$ ≒ $\frac{f(a+ h)-f(a)}{h}$
この式の分母を払うと，
f ’(a) h≒f(a+h)−f(a)
f(a+h)≒f(a)+f ’(a)h…(1)
あるいは，f(x)≒f(a)+f ’(a)(x−a)…(1)’
(1)はhの１次式であるので，１次の近似式と呼ばれる．

　これに対して，定数項f(a)だけを用いた場合，
f(a+h)≒f(a)…(0)
f(x)≒f(a)…(0)’
は0次の近似式と呼ばれる．

　数値で表わしたときの目安として，
　　　縦横比が極端でない直角三角形ができ，
　　　h=x−aが小数第1位のオーダー
ならば，0次近似はf(x)の整数部のオーダーまで，1次近似は小数第1位のオーダーまで，２次近似は小数第2位のオーダーまで信頼できると考えてよい．（誤差も hⁿのオーダーに収ることが知られている．）

○　0次近似関数

f(x)を近似するために，定数項のモデルを当てはめ，aからxまでf(x)=pの上にあるとすれば
p=f(a)だから，f(x)=pとなる．

○　1次近似関数

f(x)を近似するために，１次関数のモデルを当てはめ，aからxまでf(x)=p+qxの上にあるとすれば（以下は近似であるが，当てはめたモデルについて等号で表わす）
　　　f(a)=p+qa…(1-1)
2つの係数p,qを定めるために，もう一つ方程式を作る．
　　　f ’(a)=q…(1-2)
(1-1)（1-2)より，q=f ’(a),p=f(a)−f ’(a)a
f(x)=( f(a)−f ’(a)a )+f ’(a)x=f(a)+f ’(a)(x−a)
となる．

○　2次近似関数

f(x)を近似するために，2次関数のモデルを当てはめ，aからxまでf(x)=p+qx+rx²の上にあるとすれば
3つの係数p,q,rを定めるために方程式を3個使う．
　　　f(x)=p+qx+rx²
　　　f ’(x)=q+2rx
　　　f ”(x)=2r
この関数はaからxまで同一モデル上にあるとしているから，aの値で係数を定めると，
　　　f(a)=p+qa+ra²…(2-1)
　　　f ’(a)=q+2ra…(2-2)
　　　f ”(a)=2r…(2-3)
これより， $r=\frac{f\apos(a)}{2}$ , q=f ’(a)−f ”(a)a ,
p=f(a)−(f ’(a)−f ”(a)a)− $r=\frac{f\apos\apos(a)}{2}$ a2
代入すると，f(x)=f(a)+f ’(a)(x−a)+ $\frac{f\apos\apos(a)}{2}$ (x−a)2となる．

◇2変数関数の微分◇

１．　偏微分係数

　ここでは，多変数関数（変数が2個以上の関数）の例として2変数関数を扱う．
　2変数関数は，z=f(x , y)と書くことができ，一般に3次元空間における曲面となる．また，その微小部分は接平面すなわち平面とみなせる(右図)．

　点(a , b )の付近で曲面z=f(x , y)の様子を調べるために，y座標が一定（y=b）の点ばかりを選ぶと，z=f(x , b)はy軸に垂直（zx平面に平行）な平面上の曲線となる．
　このとき，
$\lim_{x\rightarrow a}\frac{f(x,\hspace{2}b)-f(a,\hspace{2}b)}{x-a}$

を，点(a, b)におけるxによる偏微分係数といい，

$f_x(a,\hspace{2}b)$ または $\frac{\partial f}{\partial x}(a,\hspace{2}b)$
で表わす．y座標が一定（y=b）としているから，z=f(x , b)はxだけの関数で，ここに述べた極限値は従来と同じように求めることができる．
　xによる偏微分係数 $\frac{\partial f}{\partial x}(a,\hspace{2}b)$ は，図形的には，y軸に垂直な平面y=bで切った断面におけるx=aの点における接線の傾きを表わしている．

　同様にして，x座標が一定（x=a）の点ばかりを選ぶと，z=f(a , y)はx軸に垂直（yz平面に平行）な平面上の曲線となる．　このとき，
$\lim_{y\rightarrow b}\frac{f(a,\hspace{2}y)-f(a,\hspace{2}b)}{y-b}$

を，点(a , b)におけるyによる偏微分係数といい，

$f_y(a,\hspace{2}b)$ または $\frac{\partial f}{\partial y}(a,\hspace{2}b)$
で表わす．yによる偏微分係数 $\frac{\partial f}{\partial y}(a,\hspace{2}b)$ は，図形的には，x軸に垂直な平面x=aで切った断面におけるy=bの点における接線の傾きを表わしている．

例
(1)　z=f(x , y)=2x+3y+4上で，点(1 , 2 )におけるxによる偏微分係数を求めると，y=2を代入して
z=f(x, 2)=2x+6+4=2x+10
のx=1における微分係数を求めればよいから，
$f_x(1,\hspace{2}2)=\frac{\partial f}{\partial x}(1,\hspace{2}2)=\frac{d}{dx}(2x+ 10)|_{x=1}=2$
となる．

(2)　上の例で，点(1, 2 )におけるyによる偏微分係数を求めると，x=1を代入して
z=f(1, y)=2+3y+4=3y+6
のy=1における微分係数を求めればよいから，
$f_y(1,\hspace{2}2)=\frac{\partial f}{\partial y}(1,\hspace{2}2)=\frac{d}{dy}(3y+ 6)|_{y=2}=3$
となる．

(3)　z=f(x , y)=x²+y²+1上で，点(2 , 3 )における偏微分係数を求めると
$f_x(2,\hspace{2}3)=\frac{\partial f}{\partial x}(2,\hspace{2}3)=\frac{d}{dx}(x^2+ 10)|_{x=1}$
$=2x|_{x=2}=4$
$f_y(2,\hspace{2}3)=\frac{\partial f}{\partial y}(2,\hspace{2}3)=\frac{d}{dy}(y^2+ 5)|_{y=3}$
$=2y|_{y=3}=6$

２．　偏導関数

　各々の(x , y)の値についてyを定数と見なしてxで微分したもの，及び，xを定数と見なしてyで微分したものを，各々x , yによる偏導関数（偏微分）といい，

$f_x(x,\hspace{2}y)$ または $\frac{\partial f}{\partial x}(x,\hspace{2}y)$ または $\frac{\partial z}{\partial x}$
及び
$f_y(x,\hspace{2}y)$ または $\frac{\partial f}{\partial y}(x,\hspace{2}y)$ または $\frac{\partial z}{\partial y}$
で表わす．

例
(1)　z=f(x , y)=2x+3y+4について

　　fx(x , y )=(x , y)==2

　　fy(x , y )=(x , y)==3

(2)　z=f(x , y)=x²+y²+1について

　　fx(x , y )=(x , y)==2x

　　fy(x , y )=(x , y)==2y

(3)　z=f(x , y)=5x²y³+2x−3y+4について

　　fx(x , y )=(x , y)==10xy³+2

　　fy(x , y )=(x , y)==15x²y²- 3

３．　2次偏導関数

　偏導関数をさらに微分して2次偏導関数を考えることができる．
　z=f(x , y)について，xによる偏導関数を作ってから，それのyによる偏導関数を考えるときは

()すなわち　もしくは　fxy

で表わす．
　2変数関数の2次導関数としては，次の4種類のものを考えることができる．ただし，添字で表わす場合には添字の順序の違いに注意．

()すなわち　もしくは　fxx

()すなわち　もしくは　fxy

()すなわち　もしくは　fyx

()すなわち　もしくは　fyy

多くの場合，xで偏微分してからyで偏微分しても，yで偏微分してからxで偏微分しても結果は変らない．
すなわち，

=もしくは　fxy=fyx

が成り立つ．

例
　z=f(x , y)=5x²y³+2x−3y+4について

　　()==fxx=(10xy³+2 )=10y³

　　()==fxy=(10xy³+2 )=30xy²

　　()==fyx=(15x²y²−3 )=30xy²

　　()==fyy=(15x²y²−3 )=30x²y

４．　接平面の方程式

　3次元空間において点A(a,b,c)を通り，法線ベクトル
=(p,q,r)に垂直な平面の方程式は，x , y , zの１次方程式

p(x−a )+q(y−b)+r(z−c)=0

の形で表わすことができる．

　逆に，p=q=r=0という特別な場合を除けば，px+qy+rz+d=0で表わされる図形は，3次元空間において法線ベクトル=(p,q,r)に垂直な平面を表わす．

図

特に，z−c=p(x−a)+q(y−b)の形で書かれる平面は，

p(x−a)+q(y−b)−(z−c)=0

と変形できるから，点( a , b , c )を通り，法線ベクトル=(p,q,−1)に垂直な平面を表わす．

（証明）
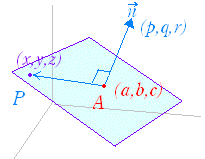
　左図のように，点A(a,b,c)を通り，法線ベクトル=(p,q,r)に垂直な平面に点P(x,y,z)があれば，⊥が成り立ち，
⊥が成り立てばP(x,y,z)は，点A(a,b,c)を通り，法線ベクトル=(p,q,r)に垂直な平面上にあるといえる．
　２つのベクトルの垂直条件は，内積が0となることであるから，

·=0

を成分で表わすと，

p(x−a )+q(y−b)+r(z−c)=0

が点A(a,b,c)を通り，法線ベクトル=(p,q,r)に垂直な平面に点P(x,y,z)があるための必要十分条件となる．
（平面から少しでも外れるとこの式が成り立たないことが分かる．）

（後半の証明）
　次に，p(x−a )+q(y−b)+r(z−c)=0は展開すれば容易に
px+qy+rz+d=0の形に直せることが分かる．

　また仮定により，p, q, rのうち，0でないものが少なくとも１つはあるから，ここではp≠0とすると，px+qy+rz+d=0は

p(x−)+q(y−0)+r(z−0)=0

の形に書けるから，法線ベクトル=(p,q,r)に垂直な平面を表わす．

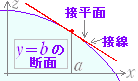
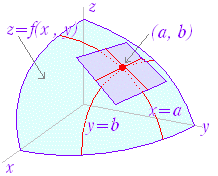
○　曲面z=f(x , y)上の点A(a,b,f(a,b))における接平面の方程式は，

z=fx(a , b )(x−a)+fy(a , b )(y−b)+f(a,b)

で表わされる．
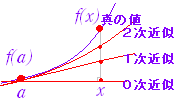
　この方程式は，点A(a,b,f(a,b))付近における関数z=f(x , y)の１次の近似式となっている．

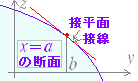
○　曲面z=f(x , y)をy軸に垂直な平面で切った断面上における接線の方程式は

z=fx(a , b )(x−a)+f(a,b)ただしy=b

で表わされる．(yを定数としてから微分したものと，接平面を求めてからyを定数としても同じ結果が得られる．)

○　曲面z=f(x , y)をx軸に垂直な平面で切った断面上における接線の方程式は

z=fy(a , b )(y−b)+f(a,b)ただしx=a

で表わされる．(xを定数としてから微分したものと，接平面を求めてからxを定数としても同じ結果が得られる．)

○　曲面z=f(x , y)上の点A(a,b,f(a,b))における等高線の接線の方程式（xy平面に平行な接線の方程式）は

fx(a , b )(x−a)+fy(a , b )(y−b)=0ただしz=f(a,b)

で表わされる．（これは接平面の方程式においてz=f(a , b)とおくと得られる．）

例
(1)　曲面z=x³+2xy−3y²のx=0 , y=1に対応する点においては，
　　　f(0 , 1 )=−3
　　　f_x(x , y )=3x²+2y , f_x(0 , 1)=2
　　　f_y(x , y )=2x−6y , f_y(0 , 1)=−6
となるから，
接平面の方程式：
　　　z=2x−6(y−1)−3=2x−6y+3
y軸に垂直な断面における接線の方程式
　　　z=2x−3ただし，y=1
x軸に垂直な断面における接線の方程式
　　　z=−6(y−1)−3=−6y+3ただし，x=0
等高線の接線の方程式
　　　2x−6(y−1)=2x−6y+6=0，x−3y+3=0ただし，z=−3

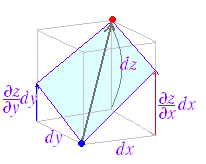
　y軸に垂直な平面で切った断面における接線の傾きは
p=(a,b)だから，接線方向のベクトルは

(1, 0 , p )

　x軸に垂直な平面で切った断面における接線の傾きは
q=(a,b)だから，接線方向のベクトルは

(0, 1 , q )

　これらはいずれも，(p , q ,−1 )と垂直である：

1·p+0·q+p·(−1)=0
0·p+1·q+q·(−1)=0

　そこで，接平面の方程式は，

p(x−a)+q(y−b)−(z−f(a,b))=0

すなわち，

z=fx(a , b )(x−a)+fy(a , b )(y−b)+f(a,b)

で表わされる．

５．　全微分

　曲面z=f(x , y)上の点A(a,b,f(a,b))における接平面の方程式

z−f(a,b)=fx(a , b )(x−a)+fy(a , b )(y−b)

において，xの増分x−aをΔx，yの増分y−bをΔy，zの増分z−f(a,b)をΔzで表わすと，

Δz=f_x(a , b )Δx+f_y(a , b )Δy

となる．この式の Δx，Δy→0となるときの極限を

dz=f_x(a , b )dx+f_y(a , b )dy

で表わし，zの全微分という．

　全微分

dz=f_x(a , b )dx+f_y(a , b )dy

あるいは，

dz=dx+dy
は，x方向にdx，y方向にdyだけ増加したときのz方向の増分を表わしている．

○===メニューに戻る