関数とは

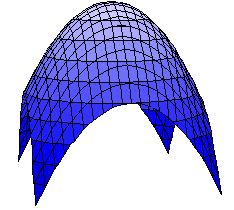
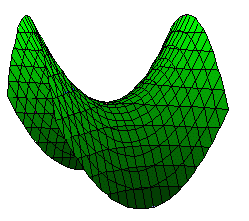
◇関数とは何か◇

　集合Aの要素に集合Bの要素を対応させる規則が与えられているとき，この対応の規則をAからBへの写像という．
　写像においては，a∈Aが定まればb∈Bが定まることが重要である．

　写像のうち，数に関する集合から数に関する集合への対応を関数という．(*)
　変数xの値を定めれば，変数yの値が定まるとき，xを独立変数といいyを従属変数という．

※　関数として，中学校，高等学校では式で書かれるものを扱ったが，自然現象や社会現象を研究する上ではもっと広く，一方を定めれば他方が定まるものと考える．その決定のメカニズムは必ずしも数式で表現できるものばかりではない．

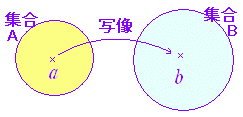※　「数に関する集合」の要素には，1 , 2 , 3 ...のような数だけでなく，座標平面上の点 (x , y) や空間における点 (x , y , z) なども含まれ，関数としては一般にRⁿ,CⁿからRⁿ,Cⁿへの対応を考える．

［記号］　aが集合Aの要素であることを，a∈Aで表わす．

［記号］　実数全体の集合をRで表わし，２次元の実数の集合をR²で表わす．
　このとき，点 (3 , −4) はR²の要素となっている．すなわち，(3 , −4) ∈R²
　同様にして，点 (−1 , 2 , 3) ∈R³

(*)　「都道府県」から「都道府県庁所在地」への対応のように数でないものと数でないものの対応は，関数ではない写像である．
　例　愛知県　→　名古屋市

　　「気温」から「天気」への対応のように，気温を定めても天気が定まらないような対応は，関数でもなく写像でもない．
　例　15°C　→　雨?，晴れ?，曇り?

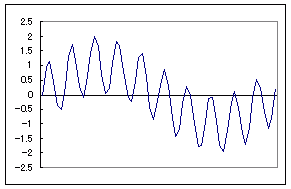
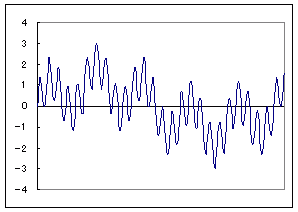
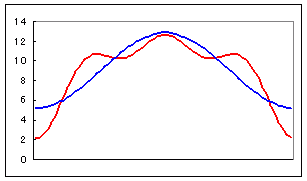
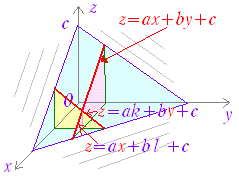
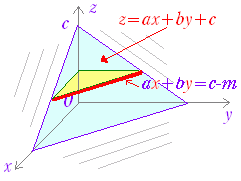
１．　対応規則が既知の数式で表せないもの
(1)　RからRへの関数の例
・　サイコロを何回も振るとき，第x回に出る目をyとするとき，xからyへの対応
・　円周率πにおいて小数第x位の数をyとするとき，xからyへの対応
・　素数を小さい方から順に並べたとき，第x番目の数をyとするとき，xからyへの対応
・　日時tから，その時点における円／ドル為替レート rへの対応

(2)　RからR³への関数の例
・　ある人について，日時tからその人のいる座標（x:東経，y:北緯，z:標高）への対応
(3)　R²からRへの関数の例
・　ある時点で（x:東経，y:北緯）からその地点を中心とする半径500m以内にいる人の数への対応
(4)　R⁴からR⁵への関数の例
・　地球の気候に関して，（x:東経，y:北緯，z:標高，t:日時）から（T:気温，P:気圧，vx:風速東向き成分，vy:風速北向き成分，vz:風速上向き成分）への対応

　問　

　左の例以外で，対応関係の数式が必ずしも明らかでない関数の例を，R→R，R→R³について１つずつ述べよ．

２．　対応規則が既知の数式で表せるもの
(1)　比例
・　y = ax(a：単価，x：個数，y：価格)
　通常の買い物では，価格は個数に比例している．

(2)　１次関数
・　y = ax+b
(携帯電話について，a：１分当り使用料，x：１か月間の利用時間（分），b：基本料金，y：１か月間の料金)

※　１次関数のグラフは直線になる．
　y = ax+bにおいて，aは傾きを表わし，a>0ならば右上がりのグラフになり，a<0ならば右下がりのグラフになる．bは切片を表わす．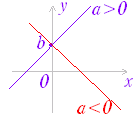

(3)　２次関数
・　y = ax²　（中学校で習う）
　a>0ならば下に凸のグラフになり，a<0ならば上に凸のグラフになる．

・　y = a(x −p)²+q　（高校で習う）
　　はy = ax²をx軸の正の向きにp,y軸の正の向きにqだけ平行移動したもので，頂点の座標は (p,q) になる．

・　一般の２次関数y = ax²+bx + cと２次関数の標準形
y = a(x −p)²+qは，お互いに他方に変形できる．

・　２次関数y = a(x −p)²+qは，
　　　a>0のときx=pにおいて最小値qをとる．
　　　a<0のときx=pにおいて最大値qをとる．

※　自然現象や社会現象において人間が最も関心を持っている最大値や最小値が存在するところが，２次関数の特徴．

※　１次関数や２次関数は，中学校，高校で習ったものであるが，微分や微分方程式において微小区間における近似式を考えるときには，ほとんどの問題がこれらで解決でき，基本的な関数となっている．

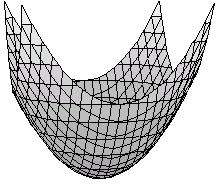
※　２次関数のグラフは，下に凸（谷形）または上に凸（山形）の放物線になる．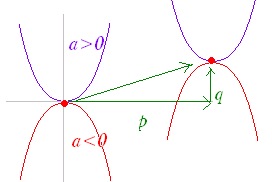

（２次関数の例）
　A版の用紙において，横（ここでは短い方の辺とする）の長さをxとすると，縦の長さyはy= $\sqrt{2}$ x，面積Sは S=xy= $\sqrt{2}$ x2となるから，面積Sは横の長さxの２次関数で表せる．

◇写像，関数と対応◇

［記号と用語］

　以下においては，集合Aの要素に対して，集合Bの要素が２つ以上対応しているようなもの（多価関数という）は考えず，集合Aの要素に対して，集合Bの要素が１つ対応する場合のみを扱う．

○　集合Aの任意の要素aに対して，集合Bの要素bが「ただ一つ定まる」（存在かつ一意）とき，この対応を写像という．

○　集合Aから集合Bへの写像fは
f：A→B などと書かれる．

○　写像f：A→Bにおいて，Aの要素aにBの要素bが対応しているとき，bを像といい，aを原像という．

○　写像f：A→Bにおいて，Aを定義域という．変数xが集合Aのすべての値をとって変化するとき，集合Bのうち像となる値の全体を値域という．

○　写像f：A→Bにおいて，値域が集合Bの全体となっているものをBの上への写像という．（全射ともいう．）
　上への写像となるための必要十分条件は，
「　Bの任意の要素bに対して，f(a)=bとなるAの要素a　が定まる　」ことである．

○　写像f：A→Bにおいて，Aの異なる要素にはBの異なる要素が対応するものを１対１の写像という．（単射ともいう．）
　１対１の写像となるための必要十分条件は，
「x₁≠x₂　ならば　f(x₁)≠f(x₂)」あるいは，その対偶をとって，
「f(x₁)=f(x₂)　ならばx₁=x₂」と表せる．

○　上への写像であって，かつ，１対１の写像となっているものを上への１対１の写像という．（全単射ともいう．）
　上への１対１の写像となるための必要十分条件は，
「　Bの任意の要素bに対して，f(a)=bとなるAの要素aがただ1つ定まる　」ことである．

■　ここでは多価関数などは考えていない．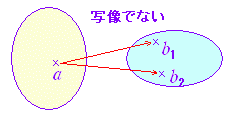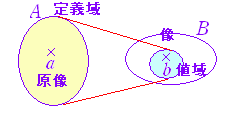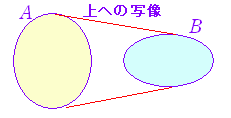

■　定義域，値域，原像，像

■　上への写像

■　１対１の写像

１対１の写像でない例：
　f：R→Rの写像（関数） f(x)=x² については，b>0について，a²=bとなるaは， a=± $\sqrt{b}$ となって，２つ存在する．（１つに定まらない．）
そこで，この写像（関数）f(x)=x²は１対１の写像（関数）ではない．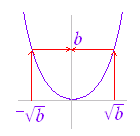

　問　
　次のグラフによって，集合Aの要素に集合Bの要素を対応させるとき，この対応は次のうちどれに該当するか．（正しい選択肢をクリックせよ）（なお，例えば，「１対１の上への写像」の場合，「写像」にも「１対１の写像」にも，「上への写像」にも該当するが，最も狭い範囲で「上への１対１の写像」と答えるものとする．他も同様．）

◇１変数関数と多変数関数◇ 　独立変数が１個の関数を１変数関数という．　１変数の関数は，１つの独立変数xの値に対して従属変数yの値が決まり，y=f(x)の形式にまとめることができる．　１変数の関数では，上に述べた１次関数，２次関数の他，指数関数，対数関数，三角関数などが自然現象，社会現象を研究する上でよく登場する．１．　指数の爆発（小話1）　日本の国内法では極端な高利貸しは，法律で禁止されているが，闇世界では窮状に乗じて暴利をむさぼる者がいると言われている．トイチとは10日で１割の利息を取る闇の高利貸しを言う．そこで，このトイチからある日１円を借りたとき，10年後に何円の借金となっているか試算してみると： 10日後=1+0.1=1.1円 20日後=1.1+1.1×0.1=1.21=1.1²円 30日後=1.21+1.21×0.1=1.331=1.1³円・・・ 100日後=1.1¹⁰=2.593円・・・ 500日後=1.1⁵⁰=117.39円・・・ 1000日後1.1¹⁰⁰=13780.6円･･･ 10年後=3650日後=1,283,305,580,313,380=1283兆円となり，日本の国家予算の何年分も必要となる．（log₁₀1.1³⁶⁵=15.1となって16桁の数となることが，確かめられる．）　(*桁数の求め方↓) （小話２）　豊臣秀吉の時代に「曽呂利新左衛門」という人がいて，あるとき，秀吉から何でもほしいものをもらえることになった．そこで新左衛門は100畳の畳を示して，１日目には1つの畳に１粒の米を，次の日には隣の畳に２粒の，さらに次の日にはその隣の畳に４粒の米を，･･･というように２倍ずつ米粒を置いてもらえばこれをいただきますと言ったという．　初めは少なく見えるが，1+2+2²+2³+・・・2⁹⁹=2¹⁰⁰-1個の米粒は，途方もなく多い．2を100乗もすると日常生活で使わないような桁外れの数字ができてしまう．　1粒の米が0.02g=0.00002kg=0.00000002tとすると， 0.00000002×(2¹⁰⁰-1) ここで 2¹⁰=1024≒1000，2¹⁰⁰=(2¹⁰)¹⁰=(10³)¹⁰=10³⁰として概算すると，少なめに見積もって 2×10^-8×10³⁰=2×10²²t 　今日の生産力でも世界全体で米の生産高は，年間約6億=6 0000 0000tと言われており，はるかに及ばない．(右上に続く→)	（→続き）　問　　（小話2）において，畳50畳であれば秀吉は合計何トンの米を渡さなければならなかったか．米１粒を0.02gとして概算で示せ．　Check
	（小話３）　幼い子には知り合いが少なく，有名な政治家には知り合いが多いが，ここでは誰でも１00人の知り合いがいるものとする．また簡単にするために，知り合いを友達と言い換える．このとき，世界中どの２人をとっても，どちらか一方から，友達の友達の友達を選び，他方からも，友達の友達を選べば，同じ人になることを示すことができる．　すなわち，ある人の友達は100人あり，こちらから３回，先方から2回考えると，合計5ステップある．これは，こちらから100倍ずつの5ステップを考えても同じだから，合計100⁵=100 0000 0000=100億人に及ぶ．　ところが世界の人口は約66億人といわれており，100億もあれば世界の人口をカバーできるので5ステップあれば世界中の誰とでもつながる．（もちろん，6人家族で閉じているような短いルートもあるが，遠方に到達する長いルートが少なくとも１つは存在するという意味である．ただし，重なりは無視する．）　そこで，一方の端を自分として，他方の端を「アメリカ大統領」としても，また「ローマ法王」としても，友達の友達の友達は，友達の友達だと言っても，相手が同時代の人なら，ほら吹きとはならない．（小話４）　マラカイトグリーンと呼ばれる緑色の薬品は，主に観賞魚の皮膚病の治療に用いられるが，食用魚に用いることは禁止されている．　さて，この薬品は原液を25万倍に薄めて用いることになっている．では，どのようにして25万倍に薄めるか．･･･まず，1mLの原液に水を加えて500mLにすると，これで500倍に薄まる．次に，そのできた液のうち1mLだけを取り出して，これに水を加えて500mLにすると，２回の操作で500×500=250000となり，500mLのビーカーと1mLの小さじがあれば25万倍に薄めることができる．
	問　　食塩58gの中には，6×10²³個の塩化ナトリウムの分子が含まれる．食塩58ｇを500mLの水に溶かしたものを食塩水の原液とするとき，（小話4）の要領で薄めていき，塩化ナトリウムの分子がちょうど1個含まれる液体を作るには，何回薄めればよいか．（実際には，薄めるのに用いる水［それ自体が全く塩分を含まない水］を入手することは難しく，よくかき回して均一な濃度にするのも難しいが，ここでは理屈通りに実験が進むものとして試算してみよ．）　Check

２．　自然対数の底，指数関数，対数関数

(1)

次の極限値により自然対数の底eを定義する．
$\lim_{n\rightarrow\infty}(1+\frac{1}{n})^n=e$ （nは整数）

（この極限値は約2.71828...）

このとき，次の性質が成り立つ．

1)　 $\lim_{n\rightarrow\infty}(1-\frac{1}{n})^{-n}=e$ 　（nは整数）

2)　 $\lim_{x\rightarrow 0}(1+ x)^{\frac{1}{x}}=e$ 　　（xは実数）

3)　 $\lim_{h\rightarrow 0}\frac{\log(1+ h)}{h}=1$ 　　（hは実数，底はe）

4)　 $\lim_{h\rightarrow 0}\frac{e^h-1}{h}=1$ 　　（hは実数）

5)　y=ex　→　y’=ex
6)　 $y=\log_ex$ 　→　 $y\apos=\frac{1}{x}$

（小話）　なるべく有利に利息を得るには

　以下のような条件で預金の利息を有利に得る方法を考える．

　最近では同一銀行でも預金の出し入れに手数料が必要な場合もあるが，ここでは手数料は考えないものとする．
　数字が小さいと分かりにくいので，ここでは年利率100％として，1万円預ける場合を考える．
　途中解約の場合は，利息は預けた期間に比例して計算されるものとする．

　単純に１年間預けた場合，元金1万円+利息1万円で元利合計2万円となる．
　しかし，半年後に引き出した場合，利息は半分になるので，元金1万円+利息0.5×1万円で，元利合計1.5万円となり，これをもう一度預け入れると，残り半年間1.5万円を預けるので，元金1.5万円+利息1.5×0.5万円，元利合計は1.5+1.5×0.5=1.5²=2.25万円となり，単純に１年間預けたときと比べて有利になっている．

　そこで，さらにもっと細かく出し入れすることにし，4か月（1/3年）ごとに出したり入れたりすると，4か月目には1+1/3万円出して直ちに預け，8か月目には，(1+1/3)+(1+1/3)*1/3=(1+1/3)²万円を出して直ちに預け直すと，１年目には(1+1/3)³=2.37万円となる．

　このようにして，入れたり出したりを小刻みに行うほど有利になるので，限りなく細かく財産管理を行い，１秒ごとに出し入れすることまで考えると，１万円の元金の運用で一財産稼げるかのように思われるが，果たしてどうなるか．
　１年間をn等分して出し入れすることにすれば，１回について期間は $\frac{1}{n}$ 年なので元利合計が $1+\frac{1}{n}$ 倍になることに注意すると，これをn回繰り返すことにより $(1+\frac{1}{n})^n$ 倍となる．そこで，限りなく細かく分割して出し入れすると，
$\lim_{n\rightarrow\infty}(1+\frac{1}{n})^n=e$ を求めることになる．
　この式の値は，nが大きくなるにつれて増加する数列となっているが，nが大きくなってくると増え方が緩くなり，一定の値に収束する．この値が 2.71828...で記号eで表わされる．

(右上に続く→)

(→続き)
（eの定義を用いた，1)〜6)証明）
1)←：
$\lim_{n\rightarrow\infty}(1-\frac{1}{n})^{-n}=\lim_{n\rightarrow\infty}(\frac{n-1}{n})^{-n}$
$=\lim_{n\rightarrow\infty}(\frac{n}{n-1})^n=\lim_{n\rightarrow\infty}(1+\frac{1}{n-1})^n=e$

2)←：
左下のグラフのように $(1+\frac{1}{x})^x$ は単調増加関数で，
nを整数として，n≦xのとき， $(1+\frac{1}{n})^n\underline{\le}(1+\frac{1}{x})^x\underline{\le}e$
だから
$\lim_{x\rightarrow\infty}(1+\frac{1}{x})^x=e$
がいえる．

1)から，同様にして
$\lim_{x\rightarrow-\infty}(1+\frac{1}{x})^x=e$
がいえる．
そこで， $\frac{1}{x}=t$ とおくと，
$\lim_{x\rightarrow+ 0}(1+ x)^{\frac{1}{x}}=\lim_{t\rightarrow+\infty}(1+\frac{1}{t})^t=e$
$\lim_{x\rightarrow-0}(1+ x)^{\frac{1}{x}}=\lim_{t\rightarrow-\infty}(1+\frac{1}{t})^t=e$
の両方がいえるから，2)が成り立つ．(右極限値と左極限値が存在してそれらが一致するとき，極限値はその一致した値となる．)
3)←： 　まず，対数関数はその定義域において連続なので，
$\lim_{x\rightarrow a}f(x)=A$
のとき，
$\lim_{x\rightarrow a}\log f(x)=\log A$
となることに注意する．

　次に，
$\lim_{h\rightarrow 0}\frac{\log(1+ h)}{h}=\lim_{h\rightarrow 0}\frac{1}{h}\log(1+ h)$
$=\lim_{h\rightarrow 0}\log(1+ h)^{\frac{1}{h}}$
ここで2)により，
$\lim_{h\rightarrow 0}(1+ h)^{\frac{1}{h}}=e$
であるから，対数関数の連続性により
$=\lim_{h\rightarrow 0}\log(1+ h)^{\frac{1}{h}}=\log e=1$

4)←：
$e^h-1=t$
とおくと
$e^h=t+ 1$
$h=\log(1+ t)$ 　（底はe）
となる．
このとき， $h\rightarrow 0$ ならば $t\rightarrow 0$ だから（∵ $e^0=1$ ）
$\lim_{h\rightarrow 0}\frac{e^h-1}{h}=\lim_{t\rightarrow 0}\frac{t}{\log(1+ t)}$
は3)により1となる．

5)←：
$\lim_{h\rightarrow 0}\frac{e^{x+ h}-e^x}{h}=e^x\lim_{h\rightarrow 0}\frac{e^h-1}{h}$
は4)によりexとなるから，
y=ex→y’=exが成り立つ．

6)←：
$\lim_{h\rightarrow 0}\frac{\log(x+ h)-\log x}{h}=\lim_{h\rightarrow 0}\frac{\log(1+\frac{h}{x})}{h}$
$=\lim_{h\rightarrow 0}\frac{\log(1+\frac{h}{x})}{\frac{h}{x}}\cdot\frac{1}{x}=\frac{1}{x}$

　問　
　次の極限値を求めよ．(選択肢から選べ．)

　桁数の非常に大きな数はその全部を求めることが難しいときでも，桁数は10を底とする対数：常用対数で求めることができる．
　常用対数については，次の性質が成り立つ．（解説→※）

　n≦log₁₀X<n+1のとき，Xの整数部分はn+1桁である．

例
log₁₀X=0.002ならXは１以上10未満の数となる．
log₁₀X=1.502ならXは１0以上100未満の数となる．
log₁₀X=2.987ならXは１00以上1000未満の数となる．
....
log₁₀X=8.0123ならXは１億以上10億未満の数となる．

（※）

元の数X	1	10	100	…	10^n-1	10ⁿ
log₁₀X	0	1	2	…	n-1	n
整数部分の桁数	1	2	3	…	n	n+1

例
log₁₀1000=3　，log₁₀10000=4　だから，1000≦X<10000ならば3≦log₁₀X<4となり，4桁の整数の常用対数の整数部分は3になる．

　逆に，log₁₀Xがnならば元の数Xは整数部分がn+1桁になる．
例
2¹⁰⁰の桁数を求めるためには，その常用対数を計算すればよく，log₁₀2¹⁰⁰=100 log₁₀2=100×0.3010=30.1
だから，2¹⁰⁰は31桁の整数だと分かる．

(2)　指数計算

　p，q を有理数（正負の整数や分数）とするとき，次の指数法則が成り立つ．これを用いて，次の問に答えよ．
　　 (1)　apaq= ap+q　　(2)　　ap÷aq=ap-q
　　 (3)　(ap)q=apq
　　 (4)　(ab)p=apbp　　　(5)　 $(\frac{a}{b})^p=\frac{a^p}{b^p}$

※　指数法則の基本については，［→このページ←］参照

例
　3.5×1.7÷2.3を有効数字２桁で計算すると2.6になる．このとき，
(3.5×105)×(1.7×10−3)÷(2.3×104)
=2.6×105+( −3) −4
=2.6×10−2となる．

（参考） Microsoft Excelにおいて，（標準形式で）数値が横幅に収まらないとき，
大きな数：a.bcd×10n　は　a.bcd E+n
小さな数：a.bcd×10−m　は　a.bcd E −mと表示される．

(3)　対数計算

　底a＞0，a≠1，真数＞0のとき，対数は次の性質を満たす．計算に当たっては，(3)〜(6)で変形し，(1)(2)に持ち込むとよい．

(1)　log_a1=0　　　(2)　log_aa=1
(3)　log_aMN = log_aM + log_aN
(4)　 $\log_a\frac{M}{N}=\log_aM-\log_aN$

(5)　log_aMn = n log_aM
(6)　 $\log_ab=\frac{\log_cb}{\log_ca}$

例
log₁₀2=0.3010 , log₁₀3=0.4771のとき，
log₁₀5=log₁₀10 −log₁₀2=0.6990
log₁₀15=log₁₀5+log₁₀3=0.6990+0.4771=1.1761

　問　

３．　三角関数　三角関数の性質については，高校以来さまざまな側面から学んでいるが，ここでは「周期，振幅」「偶関数，奇関数」「第2次導関数の特徴」について，補足説明する． (1)　周期，振幅　y=sin xのグラフは右図のようになる．山の高さ（正の値）を振幅といい，山から山（または谷から谷）までの長さを周期という．一般に，任意のxについて， f(x+p)=f(x) が成り立つとき，f(x)は周期pの周期関数であるという．　f(x+p)=f(x)が成り立つ最小の正の数pを基本周期という．（基本周期のことを単に周期ということがある．）　基本周期pの任意の整数倍np（nは整数）は周期となる． ∵　f(x+p)=f(x)→f(x+2p)=f((x+p)+p))=f(x+p)=f(x) 　同様にして，f(x+3p)=f(x)などが示され，一般に f(x+np)=f(x) が成り立つ．　　f((x −p) +p)=f(x −p)となるから，f(x)=f(x −p) 　一般に，f(x)=f(x −np)も成り立つ．	○　y=sin xの基本周期は2πである． →sin(x+2π)=sin x →sin(x+4π)=sin x →sin(x+6π)=sin x 　･･･ →sin(x+2nπ)=sin x　が成り立つ． ○　y=cos xの基本周期も2πである． →cos(x+2π)=cos x 　･･･ →cos(x+2nπ)=cos x　が成り立つ． ○　y=tan xのグラフには山や谷はないが，同じ形が繰り返される最小の正の数はπで，周期はπとなる．
y=sin nx，y=cos nxの（基本）周期は， $\frac{2\pi}{n}$ y=tan nxの（基本）周期は， $\frac{\pi}{n}$ ∵　sin(n(x+p))=sin nxすなわちsin(nx+np)=sin nx となる最小の正の数pを求めると，np=2πより， $p=\frac{2\pi}{n}$ y=cos nx，y=tan nxについても同様． ○ 　y=sin 2xの周期はπ，　y=sin 3xの周期は $\frac{2\pi}{3}$ ，　y=sin 4xの周期は $\frac{\pi}{2}$ ，・・・のようにnを大きくすると，周期は短くなることに注意．逆に，　y=sin $\frac{x}{2}$ の周期は4π，　y=sin $\frac{x}{3}$ の周期は6π，　y=sin $\frac{x}{4}$ の周期は8π，･･･のようにnを小さくすると，周期は長くなることに注意． ※　いろいろな周期の三角関数の和として作られる関数は，繰り返し模様となる．右の２つの図は各々 y=sinx+sin10x，y=sinx+sin5x+sin25xのグラフで，短い周期と長い周期が組み合わされていることが分かる．　逆に，繰り返し模様となっているグラフは， y=a+bsinx+csin2x+dsin3x+… の形で近似することができる．(y=a+bcosx+ccos2x+…でもよい．) 　細かな模様を再現するには，多くの係数a , b , c , …を要するが，そこそこの精度で再現するには少ない個数の係数a , b , c , …でよい．（JPEG画像の圧縮比（画質）は，この係数を幾つ使うかということに関係している．）	図図
例　右図のような立体で鼻を通る断面（赤で示した線）を三角関数の１次結合（定数倍とそれらの和）で近似することを考える．（0≦x≦2πの区間でxの関数として表わす．）　右図下において，赤で示した曲線は y=18.03 −3.8 cos x −1.6 cos 2x −1.5 cos 3x の関数のグラフで，係数の大きさ（振幅）で比較するとcos xの影響が最も大きいことが分かる．　青で示した曲線は，定数項とy=cos xだけで近似したときのグラフ y=18.03 −3.8 cos x で，この断面のおおまかな特徴が捉えられている．

(2)　偶関数，奇関数

1) 任意のxについて
f( −x)=f(x)　が成立する関数f(x)は偶関数と呼ばれ，y=f(x)のグラフはy軸に関して対称となる．

2) 任意のxについて
f( −x)= −f(x)　が成立する関数f(x)は奇関数と呼ばれ，y=f(x)のグラフは原点に関して対称となる．

右のグラフから，次のことが分かる．
○　sin( −x)= −sin xが成り立つからsin xは奇関数で，y=sin xのグラフは原点に関して対称となる．
○　cos( −x)= cos xが成り立つからcos xは偶関数で，y=cos xのグラフはy軸に関して対称となる．
○　tan( −x)= −tan xが成り立つからtan xは奇関数で，y=tan xのグラフは原点に関して対称となる．

ア)整数の積に関する性質は異なり，次の性質が成り立つ：
　奇関数×奇関数＝偶関数
　奇関数×偶関数＝奇関数
　偶関数×偶関数＝偶関数
イ) 任意の関数f(x)は，奇関数と偶関数の和で表わすことができる．

（証明）
ア)
f(x), g(x)を奇関数とすると，f(−x)=−f(x), g(−x)=−g(x)が成り立つ．
このとき，p(x)=f(x)g(x)で定義される関数は，
h(−x)=f(−x) g(−x)={−f(x)}{−g(x)}=f(x)g(x)=p(x)となるから，p(x)は偶関数となる．

　f(x)が奇関数，g(x)が偶関数のとき，f(−x)=−f(x) , g(−x)= g(x)だから，q(x)=f(x) g(x)で定義される関数は，
q(−x)=f(−x) g(−x)={−f(x)}{ g(x)}=−f(x)g(x)=−q(x)となるから，q(x)は奇関数となる．
イ)
任意の関数f(x)に対して $s(x)=\frac{f(x)+ f(-x)}{2}$ で定義される関数s(x)は $s(-x)=\frac{f(-x)+ f(x)}{2}=f(x)$ であるから偶関数となる．また， $t(x)=\frac{f(x)-f(-x)}{2}$ で定義される関数t(x)は $t(-x)=\frac{f(-x)-f(x)}{2}=-t(x)$ であるから奇関数となる．
　ここで， $f(x)=s(x)+ t(x)$ だから，任意の関数は偶関数と奇関数の和で表わされる．

　問　

　問　
次の関数を偶関数と奇関数の和として表せ．）　Check
s(x)=(x+cos x)(1+tan x)

　左のイ)の考え方で形式的に作る方法もあるが，項数が少ないので，次のように「目で見て」分けてもよい．
s(x)=x+x tan x+cos x+sin x=(xtan x+cos x)+(x+sin x)

（参考）
ア）で示した，奇×奇＝偶，奇×偶＝奇，偶×偶＝偶の性質は，次の変形から分かるように，指数の和に関する性質に対応している．
奇×奇　：　x奇数×x奇数＝x奇数+奇数＝x偶数
奇×偶　：　x奇数×x偶数＝x奇数+偶数＝x奇数
偶×偶　：　x偶数×x偶数＝x偶数+偶数＝x偶数

(3)　第2次導関数の特徴
　(sin x)’=cos x　(cos x)’=−sin x
となるから，(sin x)”=−sin x　が成り立つ．
同様に　(cos x)”=−cos x　が成り立つ．
そこで，y=sin x , y=cos x　は　y”=−yという２階微分方程式の解となっていることが分かる．

　また，(sin kx)’=kcos kx　(kcos kx)’=−k2sin kx
となるから，(sin kx)”=−k2sin kx　が成り立つ．
同様に　(cos kx)”=−k2cos x　が成り立つ．
そこで，y=sin kx , y=cos kx　は　y”=−k2yという２階微分方程式の解となっていることが分かる．

　一般に，単振動のように「変位に比例する逆向きの力が働く」運動では，方程式の解として三角関数（sin kt , cos ktなど）が登場する．

= =>　 $y=\sin\sqrt{\frac{k}{m}}t$
バネ定数k，質量mの単振動の周期は，
$2\pi\div\sqrt{\frac{k}{m}}=2\pi\sqrt{\frac{m}{k}}$
となる．（kが大きいほど速く，mが大きいほど遅くなる．）

◇多変数関数の例◇ 　多変数関数の例として，以下において２変数関数について説明する．１．　2変数の１次関数 ○　リンゴx個とミカンy個を買って箱につめてもらう場合，その価格は， z=f(x , y)=ax+by+c で表わすことができる．ここで，aはリンゴの単価，bはミカンの単価，cは箱の価格である．	○　もっと多くの品物を買うような一般の買い物や実際の社会活動では，n個の変数x₁,x₂,x₃,…,x_nを用いて， $z=f(x_1,\hspace{1}x_2,\hspace{1}\cdots\hspace{1},\hspace{1}x_n)$ $=\sum_{j=1}^n a_jx_j+ b$ と表せるものが多い．
○　z=ax+by+cのように独立変数x ,yの１次式で従属変数zが表わされる図形は３次元空間における平面になる．　右の図はxyz空間における平面z=ax+by+cの概形を描いたものである．（実際にはこの平面は無限に広がっているが，見やすくするためにx , y , z>0の部分を図示している．）ア）　x=y=0を代入すればz=cとなることから，この平面とz軸との交点の座標は，(0 , 0 , c)になることが分かる．イ）　一般に，座標軸（x軸，y軸，z軸）に垂直な平面の方程式は各々x=k , y = l , z = mの形で表わされ，これらの平面は座標軸によって垂直に串刺しされたような形になっている．ウ）　z=ax+by+cをx軸に垂直な平面x=kで切った切り口の方程式は，z=ak+by+c=by+(ak+c)となり，独立変数yの1次関数である直線となる．　　（直線z=by+(ak+c)　における直線の傾きbは上の例ではミカンの単価となっている．）　同様にして，z=ax+by+cをy軸に垂直な平面y=lで切った切り口の方程式は，z=ax+bl+c=ax+(bl+c)となり，独立変数xの1次関数である直線となる．　　（直線z=ax+(bl+c)　における直線の傾きaは上の例ではリンゴの単価となっている．）　z=ax+by+cをz軸に垂直な平面z=mで切った切り口の方程式は，m=ax+by+c → ax+by=c−mとなる．この形で作られた図は「等高線」と呼ばれ，立体を図示するときによく用いられる． ※　医療分野での，ＣＴやＭＲＩによる断層画像は，幾つもの切り口を用いて立体全体を視覚化している．
問　　京都市右京区には双岡（ならびがおか）と呼ばれる小高い丘があって，ここには徒然草の作者吉田兼好の庵があったと言われている．　この丘は，西から見ると右図上のように北の丘が少し高い．また，上から見ると右図下のような形をしている．　この山の立体構造を説明するために，東西にx軸，南北にy軸を選び，z軸を高さとして，xyz軸に垂直な断層画像各々数個を用いてこの山の形を説明せよ．西側から見た遠景

２．　２変数の２次関数

　２変数の２次関数は，一般に z=ax2+2hxy+by2+px+qy+r の形で書かれるが，標準化と呼ばれる変形により，次のいずれかの形に直すことができる．
(1)　z=Ax2+By2　（A>0 , B>0）
　　下に凸の楕円放物面と呼ばれる（右図）
※　右の図1は-1≦x≦1 , -1≦y≦1の区間において，z=x2+y2の曲面をExcelグラフを用いて等高線表示したものである．（着色は初期設定から変えてある．）

(2)　z=−Ax2−By2　（A>0 , B>0）
　　上に凸の楕円放物面と呼ばれる（右図）
※　右の図2は-1≦x≦1 , -1≦y≦1の区間において，z=−x2−y2の曲面をExcelグラフを用いて等高線表示したものである．（着色は初期設定から変えてある．）

(3)　z=Ax2−By2または，z=−Ax2+By2　（A>0 , B>0）
　　双曲放物面と呼ばれる（右図）
※　右の図3は-1≦x≦1 , -1≦y≦1の区間において，z=x2−y2の曲面をExcelグラフを用いて等高線表示したものである．（着色は初期設定から変えてある．）

　問　

　Excelグラフを用いて，図3のz=x2−y2の曲面を描画してみよ．

［手順の概略］
・　x2やy2は-1≦x≦1 , -1≦y≦1 の外側では急速に大きくなるので，データは-1≦x≦1 , -1≦y≦1程度にする方が見やすい．
・　A列に−1, -0.9,−0.8, ･･･ , 1.0 を，1行目に−1, -0.9,−0.8, ･･･ , 1.0 を入力し，セルB2に
=$A1^2-B$1^2 などと計算式を書き込み，B2:V22までコピー・ペーストする．
・　分割を増やしすぎると枠線が増えすぎて，全体に黒々としてくるので，縦横10〜20分割程度が見やすい．
・　B2:V22を選択・反転表示し（元の座標は含めず，計算で得られたz座標のみを選ぶ），グラフウィザード→色分け表示する方の等高線を選べば陰線処理（向こう側の図形が見えないようにするもの）したものが表示される．
・　20×20個のxy座標の組により右図の格子が形成される．（x座標が等しい点を結んだ線，y座標が等しい点を結んだ線が表示され，これに，等高線：z座標が等しい点を結んだ線が追加されている．）
・　グラフを右クリックし，3Dグラフを選択，仰角，奥行き，回転を調整して見やすい位置を探す．

図1

図2

図3

○=== メニューに戻る

３．　三角関数　三角関数の性質については，高校以来さまざまな側面から学んでいるが，ここでは「周期，振幅」「偶関数，奇関数」「第2次導関数の特徴」について，補足説明する． (1)　周期，振幅　y=sin xのグラフは右図のようになる．山の高さ（正の値）を振幅といい，山から山（または谷から谷）までの長さを周期という．一般に，任意のxについて， f(x+p)=f(x) が成り立つとき，f(x)は周期pの周期関数であるという．　f(x+p)=f(x)が成り立つ最小の正の数pを基本周期という．（基本周期のことを単に周期ということがある．）　基本周期pの任意の整数倍np（nは整数）は周期となる． ∵　f(x+p)=f(x)→f(x+2p)=f((x+p)+p))=f(x+p)=f(x) 　同様にして，f(x+3p)=f(x)などが示され，一般に f(x+np)=f(x) が成り立つ．　　f((x −p) +p)=f(x −p)となるから，f(x)=f(x −p) 　一般に，f(x)=f(x −np)も成り立つ．	○　y=sin xの基本周期は2πである． →sin(x+2π)=sin x →sin(x+4π)=sin x →sin(x+6π)=sin x 　･･･ →sin(x+2nπ)=sin x　が成り立つ． ○　y=cos xの基本周期も2πである． →cos(x+2π)=cos x 　･･･ →cos(x+2nπ)=cos x　が成り立つ． ○　y=tan xのグラフには山や谷はないが，同じ形が繰り返される最小の正の数はπで，周期はπとなる．
y=sin nx，y=cos nxの（基本）周期は， $\frac{2\pi}{n}$ y=tan nxの（基本）周期は， $\frac{\pi}{n}$ ∵　sin(n(x+p))=sin nxすなわちsin(nx+np)=sin nx となる最小の正の数pを求めると，np=2πより， $p=\frac{2\pi}{n}$ y=cos nx，y=tan nxについても同様． ○ 　y=sin 2xの周期はπ，　y=sin 3xの周期は $\frac{2\pi}{3}$ ，　y=sin 4xの周期は $\frac{\pi}{2}$ ，・・・のようにnを大きくすると，周期は短くなることに注意．逆に，　y=sin $\frac{x}{2}$ の周期は4π，　y=sin $\frac{x}{3}$ の周期は6π，　y=sin $\frac{x}{4}$ の周期は8π，･･･のようにnを小さくすると，周期は長くなることに注意． ※　いろいろな周期の三角関数の和として作られる関数は，繰り返し模様となる．右の２つの図は各々 y=sinx+sin10x，y=sinx+sin5x+sin25xのグラフで，短い周期と長い周期が組み合わされていることが分かる．　逆に，繰り返し模様となっているグラフは， y=a+bsinx+csin2x+dsin3x+… の形で近似することができる．(y=a+bcosx+ccos2x+…でもよい．) 　細かな模様を再現するには，多くの係数a , b , c , …を要するが，そこそこの精度で再現するには少ない個数の係数a , b , c , …でよい．（JPEG画像の圧縮比（画質）は，この係数を幾つ使うかということに関係している．）	図図
例　右図のような立体で鼻を通る断面（赤で示した線）を三角関数の１次結合（定数倍とそれらの和）で近似することを考える．（0≦x≦2πの区間でxの関数として表わす．）　右図下において，赤で示した曲線は y=18.03 −3.8 cos x −1.6 cos 2x −1.5 cos 3x の関数のグラフで，係数の大きさ（振幅）で比較するとcos xの影響が最も大きいことが分かる．　青で示した曲線は，定数項とy=cos xだけで近似したときのグラフ y=18.03 −3.8 cos x で，この断面のおおまかな特徴が捉えられている．

◇関数とは何か◇

◇写像，関数と対応◇

◇１変数関数と多変数関数◇

◇多変数関数の例◇