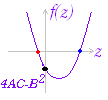◇２次関数による近似◇

→ スマホ版は別頁

◇２次関数による近似（１変数関数）◇

◇要点◇ ※　近似式に関する記述は→第２章←

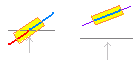
○x≒aにおける関数f(x)の振舞い

0次近似：f(x)≒f(a)

１次近似：f(x)≒f(a)+f’(a)(x−a)

２次近似：f(x)≒f(a)+f’(a)(x−a)+(x−a)2

○　特に，x≒0のとき

0次近似：f(x)≒f(0)

１次近似：f(x)≒f(0)+f’(0)x

２次近似：f(x)≒f(0)+f’(0)x+x2

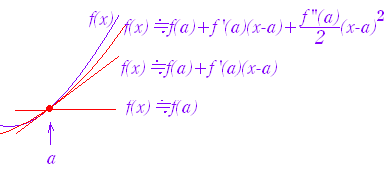※　近似式の身近な例
f(a)=1，f’(a)=2，f ”(a)=6，x−a=0.1のとき，

f(x)≒1+2·0.1+·0.12=1.23

f(a)は整数部分に対応

f’(a)(x−a)は小数第1位に対応

(x−a)2は小数第2位に対応している．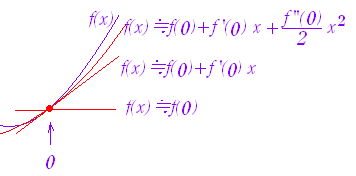

※　近似式の身近な例

f(0)=1，f’(0)=2，f ”(0)=6，x=0.01のとき，

f(x)≒1+2·0.01+·0.012=1.0203

f(0)は整数部分に対応

f’(0)xは小数第2位に対応

x2は小数第4位に対応している．

◇極値の判定◇

　以下においては，関数f(x)として滑らかな関数，すなわち，f’(x)が連続な関数のみを取り扱う．

　第4章では，x=aの前後におけるf’(x)の符号の変化によって極値の判定を行った：

○極値→f ’(x)=0でかつf ’(x)の符号が変化する
f ’(x)　の符号が正から負へ変化：極大値 f ’(x)　の符号が負から正へ変化：極小値○f ’(x)=0でもf ’(x)の符号が変化しないとき極値でない

　次のようにx=aにおけるf ”(x)の値f ”(a)で調べることもできる：

f ’(a)=0のとき，
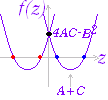
○f ”(a)>0→x=aで極小値をとる．
○f ”(a)<0→x=aで極大値をとる．
○f ”(a)=0→x=aで極値かどうかこれだけでは分からない．
※　2次導関数が負→極大，正→極小であることに注意

（証明）
　２次近似：f(x)≒f(a)+f’(a)(x−a)+(x−a)2
の式において，f’(a)=0のとき，

f(x)−f(a)≒(x−a)2

となるから，
(1)f’(a)=0, f ”(a)<0のとき，x≠aのときf(x)< f(a)となる．
(2)f’(a)=0 , f ”(a)>0のとき，x≠aのときf(x)> f(a)となる．
(3)f’(a)=0 , f ”(a)=0のとき，これだけでは分からない．

極大値

x		a
f ’(x)	＋	0	−
f(x)		f(a)

極小値

x		a
f ’(x)	−	0	＋
f(x)		f(a)

極値でない

x		a
f ’(x)	＋	0	＋
f(x)		f(a)

極大値

x		a
f ’(x)		0
f ”(x)		−
f(x)		f(a)

極小値

x		a
f ’(x)		0
f ”(x)		＋
f(x)		f(a)

これだけでは分からない

x		a
f ’(x)		0
f ”(x)		0
f(x)	?	f(a)	?

※これだけ（第2次導関数まで）では分からないとは，「分からない」ということではなく，さらに高次の導関数を用いれば判断できる．

　右の表において，ア）では，f’(a)=0 , f ”(a)=0となっており第2次導関数までだけでは極値かどうか判断できない．

　まず，符号の変わり目ではわずかな値の変化でも符号が変るが，x=aにおいて符号が正のとき，その近くにおいては，符号が急に変化するわけではないことに注意する．

○　右の表において，f ”(x)という関数の導関数はf(3)(x)で，増加して（f(3)(x)>0）0になる（f ”(x)=0）のだから，それまではf ”(x)は負であったといえる．また，0から増加するのだから，その後は正であるといえる．
　以上により，f ”(x)の符号が定まる．
○　同様にして，f’(x)という関数の導関数はf ”(x)で，減少して（f ”(x)<0）0になる（f’(x)=0）のだから，それまでは正（f’(x)>0）．また，0から増加するのだから，その後は正であるといえる．
　以上により，f’(x)の符号が定まる．
○　以上により，f(x)は増加→（休み）→増加となるから，x=0のときf(x)は極値ではないことが分かる．

※　右の表ウ）では，第3次導関数まで符号が0で第4次導関数で符号が正になる点x=0において，極小値となる例を示している．考え方は同様である．

ア）f(x)=x³

x
f ’(x)=3x²
f ”(x)=6x
f(x)	?	?

イ）f(x)=x³

x		0
f(x)		0
f ’(x)=3x²	＋	0	＋
f ”(x)=6x	−	0	＋
f(3)(x)=6	+	＋	+

ウ）f(x)=x⁴

x		0
f(x)		0
f ’(x)=4x³	-	0	+
f ”(x)=12x²	+	0	+
f(3)(x)=24x	-	0	+
f(4)(x)=24	+	+	+

例
　関数f(x)=e^xsin xがx=−において極値をとるかどうか調べよ．

（答案）
f’(x)=e^xsin x+e^xcos x=e^x(sin x+cos x)
f ”(x)=e^x(sin x+cos x)+e^x(cos x−sin x)=2e^xcos x
f’(−)=0
f ”(−)>0により，x=−において極小値をとる．

　問題
f(x)=2sin x+cos2x（0<x<π）の極値を調べた．正しいものを選べ．

◇２変数関数の近似◇

◇要点◇
○(x, y)≒(a, b)における関数f(x, y)の振舞い

0次近似：

f(x, y)≒f(a, b)･･･(1)

１次近似：

f(x, y)≒f(a, b)+fx(a, b)(x−a)+fy(a, b)(y−b)…(2)

２次近似：

f(x, y)≒f(a, b)+fx(a, b)(x−a)+fy(a, b)(y−b)

+{ fxx(a, b)(x−a)2+2fxy(a, b)(x−a)(y−b)

+fyy(a, b)(y−b)2}･･･(3)

○　特に，(x, y)≒(0, 0)のとき

0次近似：

f(x, y)≒f(0, 0)

１次近似：

f(x, y)≒f(0, 0)+fx(0, 0) x + fy(0, 0) y

２次近似：

f(x, y)≒f(0, 0)+fx(0, 0) x +fy(0, 0) y

+{ fxx(0, 0) x2+2fxy(0, 0) xy+fyy(a, b) y2}

１次近似までについては，第2章で述べた．

２次近似の式を
f(x, y)≒f(a, b)+fx(a, b)(x−a)+fy(a, b)(y−b)+A(x−a)2+B(x−a)(y−b)+C(y−b)2　･･･(4)
とおくと，A, B, Cは次のようにして求められる：

(4)の両辺をxで偏微分すると，
　fx(x, y)≒fx(a, b)+2A(x−a)+B(y−b)　･･･(5)
関数fx(x, y)に(2)を適用すると
　fx(x, y)≒fx(a, b)+fxx(a, b)(x−a)+fxy(a, b)(y−b)　･･･(6)
(5)(6)を比較すると，2A=fxx(a, b), B=fxy(a, b)

同様にして， (4)の両辺をyで偏微分すると，
　fy(x, y)≒fy(a, b)+B(x−a)+2C(y−b)　･･･(5)
関数fy(x, y)に(2)を適用すると
　fy(x, y)≒fy(a, b)+fxy(a, b)(x−a)+fyy(a, b)(y−b)　･･･(6)
(5)(6)を比較すると，B=fxy(a, b), 2C=fyy(a, b)

以上から(3)が得られる．

◇２変数関数の極値◇

　２変数関数の極値を，増減表を作成して調べる方法については第4章で学んだ．ここでは，第2次偏導関数の符号によって２変数関数の極値を調べる方法を学ぶ．
　すなわち，２変数関数f(x, y)が点(a, b)において極値をとるためには，第1次偏導関数がfx(a, b)=fy(a, b)=0を満たすことが必要条件であるが，この条件を満たしても極値でない場合が含まれる．そこで，第1次偏導関数が fx(a, b)=fy(a, b)=0を満たす点が，さらにどのような条件を満たせば極値となるかを調べる．

　上記(3)により，
f(x, y)≒f(a, b)+fx(a, b)(x−a)+fy(a, b)(y−b)+{ fxx(a, b)(x−a)2+2fxy(a, b)(x−a)(y−b)+fyy(a, b)(y−b)2}
であるが，fx(a, b)+fy(a, b)=0の場合を調べているから，
f(x, y)≒f(a, b)+{ fxx(a, b)(x−a)2+2fxy(a, b)(x−a)(y−b)+fyy(a, b)(y−b)2}
　そこで，f(x, y)−f(a, b)={ fxx(a, b)(x−a)2+2fxy(a, b)(x−a)(y−b)+fyy(a, b)(y−b)2}が，つねに正ならばf(a, b)は極小値，つねに負ならばf(a, b)は極大値といえる．

f(x, y)−f(a, b)= A(x−a)²+B(x−a)(y−b)+C(y−b)²
符号を調べると，次のことが分かる．
　ここで，A=fxx(a,b), B=fxy(a,b), C=fyy(a,b)である．

◇要点◇
(I)B²−4AC<0のとき極値となる．
　　　ア)A>0,B²−4AC<0のとき，極小
　　　イ)A<0,B²−4AC<0のとき，極大
(II)B²−4AC>0のとき極値でなく，鞍点となる．
(III)B²−4AC=0のとき，これだけでは分からない．

※　右の結果をB²−4ACの符号によって分類したものがこの要点である．

　上の結果を用いると，２変数関数の極値は次のようにまとめることができる．
※H(x, y)はヘッセ行列と呼ばれる．

◇要点◇
$H(x,\hspace{2}y)=\begin{pmatrix}f_{xx}(a,\hspace{2}b)& f_{xy}(a,\hspace{2}b)\\ f_{xy}(a,\hspace{2}b)& f_{yy}(a,\hspace{2}b)\end{pmatrix}$
とおき，
行列H(x, y)の固有値を，p,qとすると，
(I)p,qが同符号ならば，f(x, y)は(a, b)で極値をとる．
　　　p >0,q >0のとき，極小値
　　　p <0,q <0のとき，極大値
(II)p,qが異符号ならば，f(x, y)は(a, b)で極値とならず鞍点となる．
(III)pq=0のとき，f(x, y)は(a, b)で極値かどうかこれだけでは分からない．

（解説）　次のように変形する．
i)A≠0のとき，
F=A(x−a)²+B(x−a)(y−b)+C(y−b)²とおくと
F=A {(x−a)²+(x−a)(y−b) }+C(y−b)²

=A {(x−a)+(y−b) }2−(y−b)2+C(y−b)2

=A {(x−a)+(y−b) }2−(y−b)2
だから，点(a, b)の近くで
A>0, B²−4AC<0ならばF≧0(等号は(x, y)=(a, b)のとき)
A<0, B²−4AC<0ならばF≦0(等号は(x, y)=(a, b)のとき)
（0≦B²<4ACのときは，Aは0とはならない．）

B²−4AC>0ならばAと−は符号が逆になり，Fは正の値も負の値もとる：極値でなく，鞍点となる．

B²−4AC=0ならばF=A {(x−a)+(y−b) }2となり，Aの符号によって変り，これだけでは分からない．

ii)A=0のとき
F=B(x−a)(y−b)+C(y−b)²=(y−b){B(x−a)+C(y−b)}
a)B≠0のときy−bの正負に応じて，Fは正負の値をとる．

b)B=0のとき，F=C(y−b)²となり，Cの符号によって変り，これだけでは分からない．

（解説）
f(x, y)−f(a, b)={ fxx(a, b)(x−a)2+2fxy(a, b)(x−a)(y−b)

+fyy(a, b)(y−b)2}
=A(x−a)²+B(x−a)(y−b)+C(y−b)² とおくと f_xx(a, b)=2A, f_xy(a, b)=B, f_yy(a, b)=2C だから
$\begin{vmatrix}f_{xx}(a,\hspace{2}b)-z& f_{xy}(a,\hspace{2}b)\\ f_{xy}(a,\hspace{2}b)& f_{yy}(a,\hspace{2}b)-z\end{vmatrix}=0$
は，
$\begin{vmatrix}2A-z& B\\ B& 2C-z\end{pmatrix}=0$
と書ける．すなわち，固有方程式は， f(z)=z²−2(A+C)z+4AC−B²=0
f(z)={ (z−(A+C) }²−(A+C)²+4AC−B²=0
f(z)={ (z−(A+C) }²−{ (A−C)²+B²}=0
となり，右のように２次関数のグラフとz軸との交点を見ると，極値かどうか調べることができる．

4AC−B²>0のとき（B²−4AC<0のとき）
0≦B²<4ACは正だから，A, Cは同符号

<===> ２つの正の固有値p,qをもつとき，上記(I)ア)より
　　　極小となる．
<===> ２つの負の固有値p,qをもつとき，上記(I)イ）より，
　　　極大となる．

4AC−B²<0のとき（B²−4AC>0のとき）

<===> 固有値が異符号となるとき，上記(II)より鞍点となる．

例1
f(x, y)=x³−3xy+y³の極値を調べよ．
（答案）
f_x=3x²−3y, f_xx=6x, f_yx=−3,f_y=−3x+3y², f_yy=6y
だから，
$H(x,\hspace{2}y)=\begin{pmatrix}6x& -3\\ -3& 6y\end{pmatrix}$
連立方程式f_x=3x²−3y=0,f_y=−3x+3y²=0の解は
(0, 0), (1, 1)の２個
(1)
(0, 0)のとき， $H(0,\hspace{2}0)=\begin{pmatrix}0& -3\\ -3& 0\end{pmatrix}$
の固有方程式は，
$\begin{vmatrix}-z& -3\\ -3& -z\end{vmatrix}=0$
固有方程式の解は，z²−9=0より，z=±3
異符号だから，(0, 0)では極値を持たず鞍点となる．

(2)
(1, 1)のとき， $H(1,\hspace{2}1)=\begin{pmatrix}6& -3\\ -3& 6\end{pmatrix}$
の固有方程式は，
$\begin{vmatrix}6-z& -3\\ -3& 6-z\end{vmatrix}=0$
固有方程式の解は，z²−12z+27=0より，z=3, 9
正の２つの解をもつから，(1, 1)で極小となり，
極小値はf(1, 1)=−1

例2
f(x, y)=sin x sin y（−<x, y<）の極値を調べよ．
（答案）
f_x=cos x sin y, f_xx=−sin x sin y,
f_yx=cos x cos y, f_y=−sin x cos y, f_yy=−sin x sin y
だから，
$H(x,\hspace{2}y)=\begin{pmatrix}-\sin x\sin y& \cos x\cos y\\ \cos x\cos y& -\sin x\sin y\end{pmatrix}$
連立方程式f_x=cos x sin y=0,f_y=sin x cos y=0の解は
(0, 0)
このとき， $H(0,\hspace{2}0)=\begin{pmatrix}0& 1\\ 1& 0\end{pmatrix}$
の固有方程式は，
$\begin{vmatrix}-z& 1\\ 1& -z\end{vmatrix}=0$
固有方程式の解は，z²−1=0より，z=±1
異符号だから，(0, 0)では極値を持たず鞍点となる．
極値はない．

　問題（半角数字=１バイト文字で答えよ）

秋の奈良

(2)f(x, y)=(x²- 2x)(y²−2y)の極値を調べよ．

（答案）
偏導関数はf_x=()(y²−2y)，f_y=(x²−2x)()，
f_xx=(y²−2y)，f_xy=(2x−2)(2y−2)，
f_yy=(x²−2x)となり，
連立方程式f_x=0，f_y=0の解は(0, 0), (1, 1), (2, 2)
ア）(0, 0)において

$H(0,\hspace{2}0)=$

$\Biggl$

$\Biggr)$

固有方程式は，

⇔z2−16=0　の解は，z=±4
だから(0, 0)において
極大値をとる極小値をとる鞍点となる
第2次偏導関数まででは極値を判別できない

イ）(1, 1)において

$H(1,\hspace{2}1)=$

$\Biggl$

$\Biggr)$

固有方程式は，

⇔(−2−z)2=0　の解は，z=2, 2
だから(1, 1)において
極大値をとる極小値をとる鞍点となる
第2次偏導関数まででは極値を判別できない

ウ）(2, 2)において

$H(2,\hspace{2}2)=$

$\Biggl$

$\Biggr)$

固有方程式は，

−z
	−z

⇔z2−4=0　の解は，z=±2
だから(2, 2)において
極大値をとる極小値をとる鞍点となる
第2次偏導関数まででは極値を判別できない

○===メニューに戻る