|
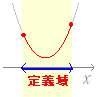
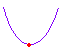
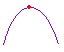
(1) 2次関数 y = ax2 (ただし,a ≠0) のグラフは, i) a>0 のとき,右図1のように下に凸(谷形)のグラフになる. ii) a<0 のとき,右図2のように上に凸(山形)のグラフになる. |
図1
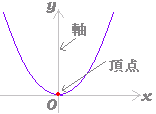 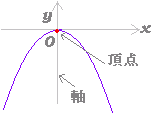 |
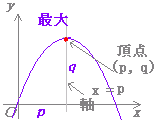
| (2) 2次関数 y = a(x−p)2 + q (ただし,a ≠0) のグラフは,右図3のように,y = ax2 のグラフをx 軸の正の向きにp ,y 軸の正の向きにq だけ平行移動したものになる. このとき,頂点の座標は (p,q) 軸の方程式は x = p となる. |
図3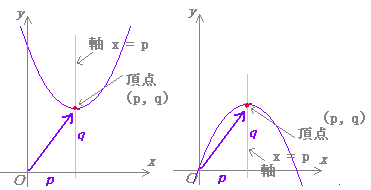 |
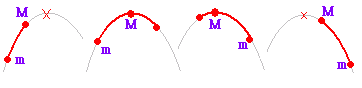
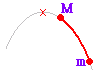
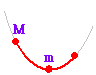
| ※ (補足説明) ・y = a(x−p)2 + q のグラフの形(上に凸か,下に凸かなど)は aの値だけで決まる. ・p,q の値は平行移動だけに関係する. ・p,q の符号に注意すること.右の例をみよ. ・2次関数のグラフの頂点は,関数の形を |
・ a>0 のとき,下に凸(谷型) ・ a<0 のとき,上に凸(山型) 例 y =2(x−3)2 + 4 のグラフは y = 2x2のグラフを x 軸の正の向きに3,yの正の向きに4だけ平行移動したもの.頂点の座標は(3,4),軸の方程式はx = 3 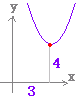 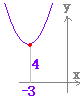 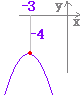 |
| ■即答問題■ ◇正しい方を選べ◇ (1) y = 2x2のグラフは ・・・→[ 上に凸 ,下に凸 ] (2) y =−2x2のグラフは ・・・→[ 上に凸 ,下に凸 ] |
◇空欄を埋めよ◇ (※以下空欄書き込み問題では,必ず「半角数字」「1バイト文字の数字」を書き込むこと) |

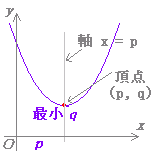 図5
図5