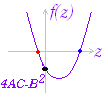◇2次関数による近似(1変数関数)◇◇要点◇
※ 近似式に関する記述は→第2章←
○x≒aにおける関数f(x)の振舞い 0次近似:f(x)≒f(a) 1次近似:f(x)≒f(a)+f’(a)(x−a) 2次近似:f(x)≒f(a)+f’(a)(x−a)+(x−a)2 ○ 特に,x≒0のとき 0次近似:f(x)≒f(0) 1次近似:f(x)≒f(0)+f’(0)x 2次近似:f(x)≒f(0)+f’(0)x+x2 |
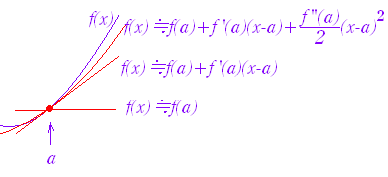 ※ 近似式の身近な例 f(a)=1,f’(a)=2,f ”(a)=6,x−a=0.1のとき, f(x)≒1+2·0.1+·0.12=1.23 f(a)は整数部分に対応 f’(a)(x−a)は小数第1位に対応 (x−a)2は小数第2位に対応している. 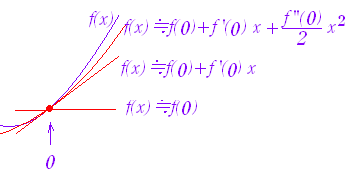 ※ 近似式の身近な例 f(0)=1,f’(0)=2,f ”(0)=6,x=0.01のとき, f(x)≒1+2·0.01+·0.012=1.0203 f(0)は整数部分に対応 f’(0)xは小数第2位に対応 x2は小数第4位に対応している. |
◇極値の判定◇以下においては,関数f(x)として滑らかな関数,すなわち,f’(x)が連続な関数のみを取り扱う.第4章では,x=aの前後におけるf’(x)の符号の変化によって極値の判定を行った: ○極値→f ’(x)=0でかつf ’(x)の符号が変化する
次のようにx=aにおけるf ”(x)の値f ”(a)で調べることもできる: f ’(a)=0のとき,
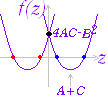
(証明)○f ”(a)>0→x=aで極小値をとる. ○f ”(a)<0→x=aで極大値をとる. ○f ”(a)=0→x=aで極値かどうかこれだけでは分からない. ※ 2次導関数が負→極大,正→極小であることに注意 2次近似:f(x)≒f(a)+f’(a)(x−a)+(x−a)2 の式において,f’(a)=0のとき,
f(x)−f(a)≒(x−a)2
となるから,(1)f’(a)=0, f ”(a)<0のとき,x≠aのときf(x)< f(a)となる. (2)f’(a)=0 , f ”(a)>0のとき,x≠aのときf(x)> f(a)となる. (3)f’(a)=0 , f ”(a)=0のとき,これだけでは分からない. |
極大値
極大値
|