4. 接平面の方程式
3次元空間において点 A(a,b,c)を通り,法線ベクトル
=(p,q,r)に垂直な平面の方程式は, x , y , zの1次方程式
p(x−a )+q(y−b)+r(z−c)=0
の形で表わすことができる.
逆に, p=q=r=0という特別な場合を除けば, px+qy+rz+d=0で表わされる図形は,3次元空間において法線ベクトル =(p,q,r)に垂直な平面を表わす.
特に, z−c=p(x−a)+q(y−b)の形で書かれる平面は,
p(x−a)+q(y−b)−(z−c)=0
と変形できるから,点 ( a , b , c )を通り,法線ベクトル =(p,q,−1)に垂直な平面を表わす. |
(証明)
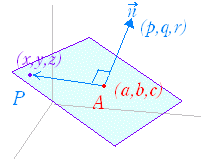
左図のように,点A(a,b,c)を通り,法線ベクトル=(p,q,r)に垂直な平面に点P(x,y,z)があれば,⊥が成り立ち,
⊥が成り立てばP(x,y,z)は,点A(a,b,c)を通り,法線ベクトル=(p,q,r)に垂直な平面上にあるといえる.
2つのベクトルの垂直条件は,内積が0となることであるから,
·=0
を成分で表わすと,
p(x−a )+q(y−b)+r(z−c)=0
が点A(a,b,c)を通り,法線ベクトル=(p,q,r)に垂直な平面に点P(x,y,z)があるための必要十分条件となる.
(平面から少しでも外れるとこの式が成り立たないことが分かる.)
(後半の証明)
次に,p(x−a )+q(y−b)+r(z−c)=0は展開すれば容易に
px+qy+rz+d=0の形に直せることが分かる.
また仮定により,p, q, rのうち,0でないものが少なくとも1つはあるから,ここではp≠0とすると,px+qy+rz+d=0は
p(x−)+q(y−0)+r(z−0)=0
の形に書けるから,法線ベクトル=(p,q,r)に垂直な平面を表わす.
|
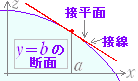
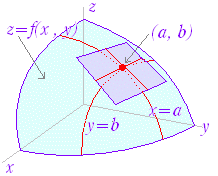
○ 曲面 z=f(x , y)上の点 A(a,b,f(a,b))における 接平面の方程式は,
z=fx(a , b )(x−a)+fy(a , b )(y−b)+f(a,b)
で表わされる.
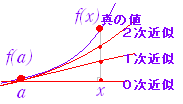
この方程式は,点 A(a,b,f(a,b))付近における関数 z=f(x , y)の 1次の近似式となっている.
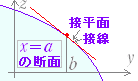
○ 曲面 z=f(x , y)を y軸に垂直な平面で切った断面上における 接線の方程式は
z=fx(a , b )(x−a)+f(a,b)ただしy=b
で表わされる. (yを定数としてから微分したものと,接平面を求めてからyを定数としても同じ結果が得られる.)
○ 曲面 z=f(x , y)を x軸に垂直な平面で切った断面上における 接線の方程式は
z=fy(a , b )(y−b)+f(a,b)ただしx=a
で表わされる. (xを定数としてから微分したものと,接平面を求めてからxを定数としても同じ結果が得られる.)
○ 曲面 z=f(x , y)上の 点 A(a,b,f(a,b))における等高線の 接線の方程式( xy平面に平行な接線の方程式)は
fx(a , b )(x−a)+fy(a , b )(y−b)=0ただしz=f(a,b)
で表わされる.(これは接平面の方程式において z=f(a , b)とおくと得られる.)
例
(1) 曲面z=x3+2xy−3y2のx=0 , y=1に対応する点においては,
f(0 , 1 )=−3
fx(x , y )=3x2+2y , fx(0 , 1)=2
fy(x , y )=2x−6y , fy(0 , 1)=−6
となるから,
接平面の方程式 :
z=2x−6(y−1)−3=2x−6y+3
y軸に垂直な断面における接線の方程式
z=2x−3ただし,y=1
x軸に垂直な断面における接線の方程式
z=−6(y−1)−3=−6y+3ただし,x=0
等高線の接線の方程式
2x−6(y−1)=2x−6y+6=0,x−3y+3=0ただし,z=−3 |
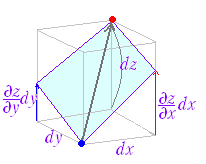
y軸に垂直な平面で切った断面における接線の傾きは
p=(a,b)だから,接線方向のベクトルは
(1, 0 , p )
x軸に垂直な平面で切った断面における接線の傾きは
q=(a,b)だから,接線方向のベクトルは
(0, 1 , q )
これらはいずれも,(p , q ,−1 )と垂直である:
1·p+0·q+p·(−1)=0
0·p+1·q+q·(−1)=0
そこで,接平面の方程式は,
p(x−a)+q(y−b)−(z−f(a,b))=0
すなわち,
z=fx(a , b )(x−a)+fy(a , b )(y−b)+f(a,b)
で表わされる.
|