定積分

== 定積分 == ○　不定積分の復習

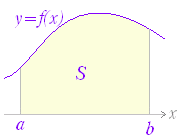
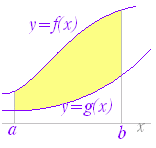
　関数 F(x)の微分がf(x)のとき，f(x)の不定積分はF(x)+Cと表せる．すなわち，

$F\apos(x)=f(x)$ のとき $\int f(x)dx=F(x)+ C$
○　曲線で囲まれた図形の面積

　図１のように，区間a≦x≦b において，曲線y=f(x)とx軸とで囲まれる図形の面積を求めるにはどうすればよいか．

　図１の面積Sを直接求める代わりに，Sの微分を求めることを考える．上の復習で分かるように，ある関数の微分が分かれば，元の関数はその不定積分で求められるからである．

　図2のように，区間の右端を変数xとして，この区間において，曲線とx軸とで囲まれる図形の面積をS(x)とおく．
ただし，曲線y=f(x)はx軸よりも上にあるものとする．

　図3のように　S(x)の増分ΔSを考えると，図4からΔSは小さい長方形と大きい長方形の間にあるから，
f(x)Δx<ΔS<f(x+Δx)Δx 　したがって，

f(x)<<f(x+Δx)

Δx→0 の極限により，微分を求めると，

f(x)≦≦f(x+Δx)=f(x)

ゆえに，

=f(x)

※　上で示した方法：

f(x)<g(x)<h(x)かつf(x)=h(x)=k
ならばg(x)=k

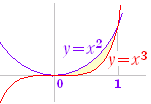
とする推論の方法を，はさみうち論法という．
　はさみうち論法において，極限移行前には不等号であっても，一般に極限値には等号が必要となる．
　すなわち， f(x)<g(x)<h(x)　→　f(x)≦g(x)≦h(x)
(簡単な例)
x>0のとき，(−x)<0<xであるが，

(−x)≦0≦x

図１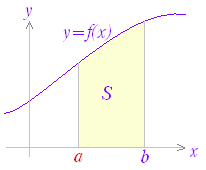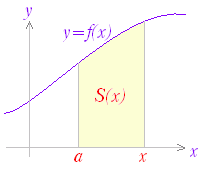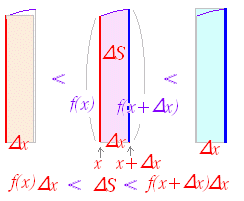

図2

図3

図4

（重要）
　面積の微分 = 縦の長さ = f(x)

　微分が f(x) になるのだから，S(x) は f(x) の不定積分となる． $S(x)=\int f(x)dx=F(x)+ C$ 　はじめに求めようとした図形は右端がx=bの場合だから， S=S(b)=F(b)+C を求めればよい．
　ここで，右端が左端に一致すれば面積は0となるから，
S(a)=F(a)+C=0
C=−F(a) 結局，

　　　　　　　　S=F(b)−F(a)

例
　曲線y=x²(1≦x≦2)とx軸とで囲まれた図形の面積は，

　　∫ n x2dx=+Cに注意すると，−= となる．

例

○　記号と用語

　上のように面積の計算をするときは，原始関数の差がつねに登場する．
　そこで，

$\int f(x)dx=F(x)+ C$

のとき，

F(b)−F(a)を $\left[F(x)\right]_a^b$ で表わす．

さらに，これを

$\int_a^b f(x)dx$

と書き，関数f(x)の定積分という．
実際に使うときは，
$\int_{a}^b f(x)dx=\Bigl[F(x)\Bigr]_a^b=F(b)-F(a)$ とする．

例
　上の例：　y=x²　(1≦x≦2)　とx軸とで囲まれた図形の面積は，
$\int_1^2 x^2dx=\Bigl[\frac{x^3}{3}\Bigr]_1^2=\frac{2^3}{3}-\frac{1^3}{3}=\frac{7}{3}$

○　定積分の計算

　上の文章では，面積と結びつけて定積分を導入したが，定積分と面積の関係は下で述べる．
　ここでは，まず，原始関数（不定積分）の差として定積分の計算に慣れることを目指す．

　右の手順に沿って，計算すればよい．ただし，不定積分の任意定数は，差で消えるので，付けなくてよい( =0)．次の２つの式を比較してみるとよい：
$\Bigl[F(x)+ C\Bigr]_a^b=\{F(b)+ C\}-\{F(a)+ C\}$
$=F(b)-F(a)$
これは，次の式と同じになる．
$\Bigl[F(x)\Bigr]_a^b=F(b)-F(a)$

※　この式でaを（定積分の）下端，b を（定積分の）上端という．

　Ｆ(上端)−F(下端)とすることが重要．（逆ではない）

例と答

　次の定積分を求めよ．

(1) $\int_1^32xdx$

（解答）
$\int_1^32xdx=\Bigl[ x^2\Bigr]_1^3=9-1=8$ …（答）

(2) $\int_0^{\frac{\pi}{2}}\sin xdx$

（解答）
$\int_0^{\frac{\pi}{2}}\sin xdx=\Bigl[-\cos x\Bigr]_0^{\frac{\pi}{2}}=0-(-1)=1$ …（答）

(3) $\int_0^{2}(e^{2x}+ e^x)dx$

（解答）
$\int_0^{2}(e^{2x}+ e^x)dx=\Bigl[\frac{e^{2x}}{2}+ e^x\Bigr]_0^{2}=\left(\frac{e^{4}}{2}+ e^2\right)-(\frac{1}{2}+ 1)$
$=\frac{e^{4}+ 2e^2-3}{2}$ …（答）

(4) $\int_0^{\frac{\pi}{2}}\sin 2x\cos 3xdx$

（解答）
$\int_0^{\frac{\pi}{2}}\sin 2x\cos 3xdx$
$=\frac{1}{2}\int_0^{\frac{\pi}{2}}(\sin 5x-\sin x)dx$
$=\frac{1}{2}\Bigl[-\frac{\cos 5x}{5}+\cos x\bigr]_0^{\frac{\pi}{2}}$
$=\frac{1}{2}\{(0)-(-\frac{1}{5}+ 1)\}=-\frac{2}{5}$ …（答）

○　定積分の性質

I)　定積分については次の性質が成り立つ．

以下，見やすくするために $\int_a^bf(x)dx$ を $\int_a^b$ と略す．
(1)　 $\int_a^a=0$
（積分区間の下端と上端が等しければ，被積分関数が何であっても定積分は0となる．）

(2)　 $\int_b^a=-\int_a^b$
（積分区間の下端と上端を入れ換えると符号が逆になる．）

(3)　 $\int_a^b=\int_a^c+\int_c^b$
（積分区間を分けて計算してよい．この式におけるcの値はa<c<bに取られることが多いが，右の解説から分かるように，この関係式はa , c , bの大小関係に関わらず成り立つ．）

II)　この他，関数の和差や定数倍について不定積分と同様に次の性質が成り立つ．
$\int_a^b\{f(x)+ g(x)\}dx=\int_a^bf(x)dx+\int_a^bg(x)dx$
$\int_a^bkf(x)dx=k\int_a^bf(x)dx$

（解説）
(1)　 $\int_a^a=\Bigl[F(x)\Bigr]_a^a=F(a)-F(a)=0$
(2)　 $\int_a^b=\Bigl[F(x)\Bigr]_a^b=F(b)-F(a)$
$\int_b^a=\Bigl[F(x)\Bigr]_b^a=F(a)-F(b)$
だから
$\int_b^a=-\int_a^b$
(3)　 $\int_a^c+\int_c^b=\{F(c)-F(a)\}+\{F(b)-F(c)\}$
$=F(b)-F(a)$
$\int_a^b=F(b)-F(a)$
したがって，これらは等しい

○　定積分と図形の面積

(1)　図5のように，区間 a≦x≦b において，f(x)≧0 を満たすとき，曲線 y=f(x) ，x軸，x=a，x=b の直線で囲まれる図形の面積S は
$S=\int_{a}^bf(x)dx$

(2)　図6のように，区間a≦x≦bにおいて，f(x)≦0を満たすとき，曲線y=f(x)，x軸，x=a，x=bの直線で囲まれる図形の面積Sは
$S=\int_a^b\{-f(x)\}dx$ これは，x軸に対称な曲線y=−f(x)(≧0)で考えると分かる．

(3)　図7のように，区間a≦x≦bにおいて，f(x)が正にも負にもなるとき，曲線y=f(x)，x軸で囲まれる図形の面積Sは
$S=\int_a^bf(x)dx+\int_b^c\{-f(x)\}dx$
これは，形式的に
$S=\int_a^c\left| f(x)\right| dx$ とまとめることができるが，実際の計算は，上のように分けて求める．

※ $\left|\int_a^bf(x)dx\right|$ とは関係ないので注意．

(4)　図8のように，区間a≦x≦bにおいて，f(x)≧g(x)≧0を満たすとき，曲線 y=f(x)，y=g(x)，直線x=a，x=bで囲まれる図形の面積Sは

$S=\int_a^b\{f(x)-g(x)\}dx$ 　　要するに $S=\int_a^b$ (上−下)dx となる．
　この関係は，y=f(x)，y=g(x)のいずれも，x軸との上下と関係なく成り立つ．
　これは，図9のように，曲線y=f(x)，y=g(x) をy軸の正の向きに平行移動して上の公式(1)で求めても，面積が変わらないからである．

図5　　　　　　　　　　　　　　　　　　　図6

図7　　　　　　　　　　　　　　　　　　　図8

図9

　(4)の公式：図8は，上に述べたすべての場合の一般的な公式となっている．

　すなわち，(1)は上の関数：y=f(x)，下の関数：y=0の差として，f(x)−0の定積分を求めていることになる．
　(2)は上の関数：y=0，下の関数：y=f(x)の差として，0−f(x)の定積分を求めていることになる．
　(3)は区間a≦x≦bにおいて，f(x)−0を，区間b≦x≦cにおいて，0−f(x)の定積分を求めていることとなる．

例と答
(1)　区間 0≦x≦π において，曲線 y=cosx とx軸とで囲まれる図形の面積を求めよ．

0≦x≦ において，cos x≧0
≦x≦π において，cos x≦0 だから

$S=\int_0^{\frac{\pi}{2}}\cos xdx+\int_{\frac{\pi}{2}}^{\pi}(-\cos x)dx$

$=\Bigl[\sin x\Bigr]_0^{\frac{\pi}{2}}+\Bigl[-\sin x\Bigr]_{\frac{\pi}{2}}^{\pi}$

$=(1-0)+(0+ 1)=2$

(2)　曲線y=x²とy=x³とで囲まれる図形の面積を求めよ．

２曲線はx=0，1で交わり，
0≦x≦1においてx³≦x²だから

$S=\int_0^{1}(x^2-x^3)dx$
$=\Bigl[\frac{x^3}{3}-\frac{x^4}{4}\Bigr]_0^{1}$
$=(\frac{1}{3}-\frac{1}{4})-(0-0)=\frac{1}{12}$

○･･･メニューに戻る