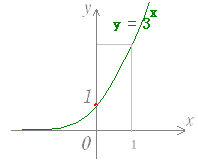
|
y=2x， y=3xなどのように指数の部分が変数になっているものを指数関数という． y=axはaを底とする指数関数と呼ばれる． y=2xのグラフは右図１のようになる． また，y=3xのグラフは右図2のようになる． 一般に，y=ax（a>1）のグラフは
i) x=0 のとき y=1 となる．
※どの指数関数のグラフも (0 , 1) を通る． ii) x → −∞ のとき y → 0 となる． ※y → −∞ ではない． iii) 右上がりで，単調増加関数となる． y=ax（0<a<1）のグラフは，図3のように右下がり（単調減少関数）となり，幾つかのaの値に対して y=axのグラフを重ねて描くと，図4のようになる． 図3   |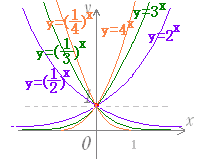
(初歩的な注意) ２次関数y=x2 と，指数関数y=2xとは全く異なる関数であるので注意すること 図1
※ x=0 における接線の傾きが，ちょうど1 となる底の値は自然対数の底と呼ばれ e=2.71828･･･となる．  |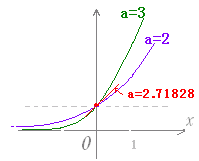
| ○ 指数関数の微分 【 要点 】 (1) i) y=ex → y’= ex ( ここに e は自然対数の底 2.71828･･･) ii) y=ekx → y’= kekx (2) y=ax → y’= ax loga |
（続き） ii) 合成関数の微分法(*1)により，
y=ax= e x loga → y’= loga・ e x loga= ax loga (*1)の補足説明 合成関数の微分法 とは： ----------- y=f(t) t=g(x) ------------------ を合成してy=f(g(x))が得られるとき，y をx で微分したものは， =
で得られる．これを合成関数の微分法という． (*2)の補足説明 ax=b y のとき，両辺の対数をとると x loga=y logb y = x loga / logb=x logba したがって ax=e y とおくと，y = x loga |
|
| [解説] （1） y=ax を導関数の定義に従って微分すると f ’(x)= = =ax =axf ’(0) （指数関数の導関数は，f ’(0) を掛ければ得られる ） 図4においてx=0 における接線の傾きが f ’(0)= =1 となる定数 a は「自然対数の底」と呼ばれ， a=2.71828･･･となる数で，指数関数，対数関数で非常に重要な働きをする．この数を e で表わす． すなわち，e=2.71828･･･のとき =1 y=ex → y’= ex ※ 対数関数の微分を先に習った場合： y=log x → y ’= を用いると y=ex → x=log y 逆関数の微分法を用いると = だから =y=ex （右上へ続く） |
||
| 例と答 次の関数を微分せよ． (1) y=e2x → y’= 2e2x (2) y=e-3x → y’= -3e- 3x (3) y=10x → y’= 10xlog 10 (4) y=xex → y’= (x+1)ex (5) y= → y’= (6) y=e- x2 → y’= -2x e- x2 |
[参考] (1) y=ekx → y’= kekx においてk=2 とする． (2) y=ekx → y’= kekx においてk=-3 とする． (3) y=ax → y’= ax loga においてa=10 とする． (4) 積の微分法を用いる． y=f(x)g(x) → y’=f ’(x)g(x)+f(x)g’(x) (5) 商の微分法を用いる． y = → y’= (6) 合成関数の微分法を用いる． y=et ，t=−x2 として = |
| ■即答問題■ |
