== 増減表,極値 ==
○ 増減表とは
右図1のようなグラフを書くときは,あらかじめ次のような増減表を作り,これに基づいてグラフを描く.
増減表は,グラフの要約となっており,増減表ができればグラフの概形(だいたいの形)は容易に描ける.
表1
|
図1
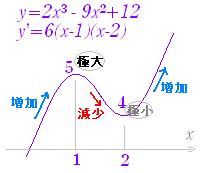 |
| ○ 増減表の作り方
y’ は接線の傾きを表わすので,y’>0 ならばyは増加,y’<0 ならば y は減少となる.
(1) 微分してy’ を求める.
(2) y’=0 となるxの値を求める.
(3) xの値,y’の符号,yの値と矢印
からなる3行の表を作る.
表は左から右,上から下へ見るものとする.
(4) (2)で求めたxの値を区切り目に入れる.
(5) y’ の符号を書き込み,y’>0ならばyは増加(上向き矢印),y’<0ならばyは減少(下向き矢印)とする.
(1) y’の符号が増加から減少に「 変化する」ところは 極大であるといい,そのときの yの値を 極大値という.
 (2) y’
(2) y’符号が減少から増加に「 変化する」ところは 極小であるといい,そのときの yの値を 極小値という.
 (3) y’=0
(3) y’=0であっても, y’の符号が正から0を通って正に戻るような場合( y’符号が変化していないところは) 極値ではない.
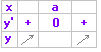 (4)
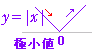
(4) 絶対値付の関数のように「折れ目」「角点」のある関数では, y’ が定義されない xの値が存在する場合がある.この場合でも, y’の符号が変化していればその点は 極値(極大値と極小値を合わせて極値という)となる.
|
y’ は接線の傾きを表わす.
 
(5) y’の符号の簡単な求め方
A) 簡単な値を実際に代入する方法
上の表1において,
x<1のときのy’の符号を求めるには,
y’=6(x−1)(x−2) に,例えばx=0 を代入するとよい.
x=0 のとき,y’=6×(-1)×(-2)=12>0
1<x<2のときのy’の符号を求めるには,
y’=6(x−1)(x−2) に,例えばx=1.5を代入するとよい.
x=1.5 のとき,y’=6×0.5×(-0.5)<0
B) 最高次の項の係数を見る方法
上の表1において,
y’=6(x−1)(x−2) は2次式で最高次の項の係数は正
y’の符号を右端を+として,順次符号を変えて埋めていく.(右から,+0-0+)
y’ が重解を持つときは,その重なりに応じて
2重ならば2回変化(=変化なし),3重ならば3回変化(=1回変化)とする.
|
例と答
(1) y=3x3−9x2の増減を調べて極値を求めよ.
(答案)
y’=9x2−18x=9x(x−2)
y’=0 となるxの値は,x=0 , 2
| x |
|
0 |
|
2 |
|
| y’ |
+ |
0 |
− |
0 |
+ |
| y |
 |
極大値
0 |
 |
極小値
−12 |
 |
x=0 のとき,極大値 y=0 をとる.
x=2 のとき,極小値 y=−12 をとる.
|
(2) y=−x4+2x2の増減を調べて極値を求めよ.
(答案)
y’=−4x3+4x=−4(x+1)x(x−1)
y’=0 となるxの値は,x=−1 , 0 , 1
| x |
|
−1 |
|
0 |
|
1 |
|
| y’ |
+ |
0 |
− |
0 |
+ |
0 |
− |
| y |
 |
極大値
1 |
 |
極小値
0 |
 |
極大値
1 |
 |
x=−1 , 1 のとき,極大値 y=1 をとる.
x=0 のとき,極小値 y= 0 をとる.
|
| (3) y=x4−4x3の増減を調べて極値を求めよ.
(答案)
y’=4x3−12x2=4x2(x−3)
y’=0 となるxの値は,x=0 (重解), 3
| x |
|
0 |
|
3 |
|
| y’ |
− |
0 |
− |
0 |
+ |
| y |
 |
0 |
 |
極小値
−27 |
 |
極大値 なし.
x=3 のとき,極小値 y=−27 をとる.
|
(4) y=−x5+の増減を調べて極値を求めよ.
(答案)
y’=x5−2x4+x3=x3(x−1)2
y’=0 となるxの値は,x=0 (三重解), 1(重解)
極大値 なし.
x=0 のとき,極小値 y=0 をとる.
|
| (5) y=x logx 増減を調べて極値を求めよ.
(答案)
y’=1·logx +x·=logx+1
y’=0 となるxの値は,x=
| x |
0 |
|
|
|
| y’ |
× |
− |
0 |
+ |
| y |
× |
 |
極小値
− |
 |
極大値 なし.
x= のとき,極小値 y=− をとる.
|
(6) y=xexの増減を調べて極値を求めよ.
(答案)
y’=ex +xex=ex(1+x)
exはつねに正.y’=0 となるxの値はx=−1
| x |
|
−1 |
|
| y’ |
− |
0 |
+ |
| y |
 |
極小値
− |
 |
極大値 なし.
x=−1 のとき,極小値 y=− をとる.
|






