順列，組合せ

→ スマホ版は別頁

■順列，組合せ■ ○　積の法則

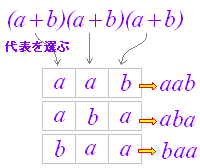
　Ａの起こり方がｍ通り，その各々についてＢの起こり方がｎ通りあるとき，ＡもＢも起こる場合の数は m×n通りある．

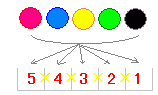
例１　図１のように，赤青黄の玉が各１個計３個あるとき，これらから２個とって，前後１列に並べる方法は何通りあるか．

　前に置く玉の選び方は，赤青黄のどれでもよいから3通り．
　その各々について，（残りの玉は２個となっているから）後に置く玉の選び方は２通り．
　結局，３×２＝６通り　

例２　図2のように，ある山の登山道が３つあるとき，この山に登って下りる方法は何通りあるか．ただし，登りと下りで同じ道は通らないものとする．

　登り道の選び方は３通り．
　その各々について，下り道の選び方が２通り．
　結局，３×２＝６通り

図1

図2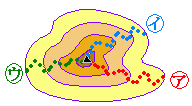

○　和の法則

　２つの事柄A，Bは同時には起こらないとする．
　Ａの起こり方がｍ通り，Ｂの起こり方がｎ通りあるとき，ＡまたはＢが起こる場合の数はm+n通りある．

例１　上の図1において，前に置く玉を赤または青と決めるとき，これら３個の玉から２個とって１列に並べる方法は何通りあるか．

(ア)　前に赤を置くとき
　　　　　後に置く方法は，青黄の２通り
(イ)　前に青を置くとき
　　　　　後に置く方法は，赤黄の２通り
(ア)(イ)は同時には起こらないから，
結局，２+２＝４通り

例２　大中小３個のさいころを投げるとき，出る目の和が15になる場合の数は何通りあるか．

　大中の目の和は右図3のようになる．
(ア)　大中の和が12となるのは1通り．このとき，小の目は3で１通り．
(イ)　大中の和が11となるのは2通り．その各々について，小の目は4で１通り．
(ウ)　大中の和が10となるのは3通り．その各々について，小の目は5で１通り．
(エ)　大中の和が9となるのは4通り．その各々について，小の目は6で１通り．
(＊)　小の目は6以下だから，大中の和が8以下のとき，出た目の和が15となることはない．
(ア)〜(エ)は同時には起こらないから，
1×1+2×1+3×1+4×1=10通り

※　「同時に起こらない」事柄とは，時間的なことではなく，論理的に両立し得ない，いわゆる「排反事象」のことをいう．

図3

大＼中和	1	2	3	4	5	6
1	2	3	4	5	6	7
2	3	4	5	6	7	8
3	4	5	6	7	8	9
4	5	6	7	8	9	10
5	6	7	8	9	10	11
6	7	8	9	10	11	12

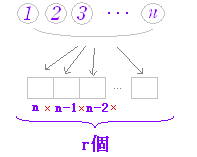
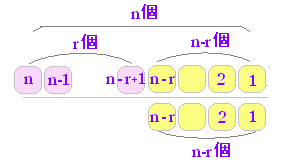
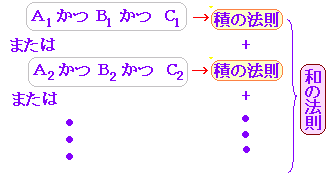
◇要約◇

　　一般に，問題を場合分けして考えるとき，「かつ」で結ばれる個々の場合に積の法則を適用し，「または」で結ばれる全体のまとめに和の法則を適用するとよい．

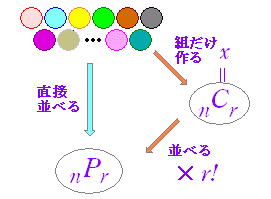
即答問題

(1)　特大，大，中，小の４個のさいころを投げるとき，目の和が21となる場合の数は何通りあるか．

(ア)　特大，大の目の和が12となるのは1通り．このとき，中，小の目の和が9となるのは4通り．　1×4＝4
(イ)　特大，大の目の和が11となるのは2通り．このとき，中，小の目の和が10となるのは3通り．　2×3＝6
(ウ)　特大，大の目の和が10となるのは通り．このとき，中，小の目の和が11となるのは通り．　
(エ)　特大，大の目の和が9となるのは通り．このとき，中，小の目の和が12となるのは通り．
(＊)　中，小の和は12以下だから，特大，大の和が8以下のときは,４個の目の和が21となることはない．
(ア)〜（エ）は同時には起こらないから，結局通り

図4

2つの和	1	2	3	4	5	6
1	2	3	4	5	6	7
2	3	4	5	6	7	8
3	4	5	6	7	8	9
4	5	6	7	8	9	10
5	6	7	8	9	10	11
6	7	8	9	10	11	12

○　階乗記号！

　正の整数および0について，階乗記号！を次のように定める．

n!=n(n-1)(n-2)···3·2·1
ただし， 0!=1 とする．

例

3!=3·2·1=6
4!=4·3·2·1=24
5!=5·4·3·2·1=120
1!=1
0! については，後に登場する順列，組合せの公式に関連して登場するときに，矛盾なく成立するように1と決める．（例外）

例
赤青黄緑黒の５個の玉を１列に並べる方法

１番目の玉の選び方は５通り
その各々について，２番目の玉の選び方は４通り
その各々について，３番目の玉の選び方は３通り
その各々について，４番目の玉の選び方は２通り
その各々について，５番目の玉の選び方は１通り
だから，５×４×３×２×１＝120通り

この問題のように，並べ方の総数を数える問題では，しばしば正の整数を大きい方から順に１まで掛け合わせたものが登場するので，これを表わす記号を作る．

10!=3628800
20!=2432902008176640000
となるなど，nが増えると，「ビックリ」するほど大きくなる．

即答問題

　右の空欄を埋めよ．

○　順列の総数

　幾つかのものを順序の違いに注意しながら１列に並べたものを順列という．

　相異なるn個のものから，r個をとって１列に並べたもの（順列）の総数を
nPr で表わす．
　このとき，
nPr=n(n-1)(n-2)···(n-r+1) 　特に，
nPn=n(n-1)(n-2)···3·2·1=n!
　また，nPrは階乗記号を用いて，次のように書ける．

$_nP_r=\frac{n!}{(n-r)!}$

例
(1)　相異なる5個のものから3個をとって，１列に並べる順列の総数は，
　　　5P3=5·4·3=60

(2)　7P4=7·6·5·4=840

(3)　4P4=4·3·2·1=24

※　階乗で計算してもよく，順にr 個掛けてもよい．

※　「r個をとる」とは，取ったものを捨てるのではなく，取ったものを使うことをいう．

※　nPr　は，nから順にr個の整数を掛けたものとなる．

※　次の図のように，n! を (n - r)! で割ると，小さい方から(n - r) 個が約分できて，r 個が残る．

即答問題

(5)　相異なる6個のものをすべて並べた順列の総数　　

(6)　相異なる5個のものから，相異なる2個をとって，１列に並べた順列の総数　　

○　組合せの総数

　順序を問題にせずに，取り出した組だけに着目したものを組合せという．

　相異なるn個のものから，相異なるr個をとった組合せの総数を

nCr

で表わす．

　このとき，

$_nC_r=\frac{n!}{r!(n-r)!}$

が成り立つ．

（解説）
　右図5のように，相異なるn個のものから，相異なるr個をとって並べる順列を２つの方法で作る．

（ア）　１つは，相異なるn個のものから，相異なるr個をとって直接並べるもので，順列の総数の公式から

$_nP_r=\frac{n!}{(n-r)!}$

となる．
（イ）　もう１つは，相異なるn個のものから，相異なるr個をとって組だけを作り，次にこれを並べるという２段階の操作で行う．このとき，順序を考えずに組だけを作る方法の総数が求める組合せの数でこれを

x=nCr

とおく．
　各々r個からなる組の並べ方は　r! 通りあるから

x× r!=nPr

よって，

$x=\frac{_nP_r}{r!}=\frac{n!}{r!(n-r)!}$

(右の例のように，各々の組合せを並べ替えると順列となる．)

図5

例
　相異なる3個の文字 a , b , c から２つ取るときの，組合せと順列の関係

組合せ	順列
{ a , b }	( a , b )
{ a , b }	( b , a )
{ a , c }	( a , c )
{ a , c }	( c , a )
{ b , c }	( b , c )
{ b , c }	( c , b )

○　よく使われる公式

　 nCn-r=nCr　･･･(1) 　
nCn=nC0=1　･･･(2)
nC1=n

（解説）
(1)　公式に当てはめて計算すれば分かる：

$_nC_{n-r}=\frac{n!}{(n-r)!\{n-(n-r)\}!}=\frac{n!}{(n-r)!r!}$

　意味から考えれば：
　上の例で考えると，３個のものから２つ選ぶとき，１つは選ばれない．これらは同数の対になっているので，１つを選んで２つが選ばれない場合の数と同じとなる．（表組の数だけ裏組がある，当りを作れば外れができる･･･世の常）

選ばれた組	選ばれない組
{ a , b }	{ c }
{ a , c }	{ b }
{ b , c }	{ a }

(2)　nCnは全部選ぶ場合で１通りある．これに対して，nC0 は空集合となり１通りになる．上の例では，次のように対応する．

選ばれた組	選ばれない組
{ a , b , c}	{ }
{ }	{ a , b , c}

例と答
　　次の値を求めよ．

(1)　 $_6C_{4}=\frac{6!}{4!2!}=\frac{6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1}{4\cdot 3\cdot 2\cdot 1\cdot 2\cdot 1}=\frac{6\cdot 5}{2}=15$

(2)　 $_7C_{2}=\frac{7!}{2!5!}=\frac{7\cdot 6\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1}{2\cdot 1\cdot 5\cdot 4\cdot 3\cdot 2\cdot 1}=\frac{7\cdot 6}{2}=21$ 　　

（参考：組合わせは整数なので，分数が残ることはない．）

(3)　 $_3C_{0}=\frac{3!}{0!3!}=1$ 　（ 0!=1 を使う）

(4)　 $_4C_{1}=\frac{4!}{1!3!}=4$ 　

即答問題

(5)　男子5人女子3人の班から男子2人女子1人の委員（役職の区別なし）を選ぶ方法は何通りあるか　通り　

(6)　A，B２人の力士が5回勝負を行うとき，力士Ａが３勝２敗となる場合の数（試合結果の星取り表）は何通りあるか．ただし，引き分けはないとする．通り　
　（※力士Ａが，5回分の番号札のうち，勝ちとなる３回分の番号札を取る方法の数を考えるとよい．［負けとなる２回の札を取っても同じ］）

○　二項定理

　(a + b)n を展開したとき，an-kbk の係数は，nCkとなる．

　すなわち，
(a + b)n =nC0 an+nC1an-1b+nC2an-2b2+…+nCn-1abn-1+nCnbn

　特に，
(1 + x)n =nC0+nC1x+nC2x2+…+nCn-1xn-1+nCnxn

（解説）
　(a + b)3 を展開したときのa2b の係数を例にとって示す．
　右図6のように，展開という事柄を，各々の（　　）から１項ずつ代表を選んで組み合わすことと考える．
　b に着目すると，これは３つの（　　）からb をとるべき1つの（　　）を選ぶ方法の数となるから，3C1=3通りとなっている．
　よって，a2b が3C1回登場するから，その係数は3C1
　一般にan-kbk の係数は，nCkとなる．

図6

例と答 (1)　(2x - 3y)5 を展開したとき，x3y2 の係数を求めよ．	一般項は， 5Ck(2x)5-k(- 3y)k k=2のとき係数は， 5C2(2)3(- 3y)2=10×8×9=720
(2)　(2x2 + 1)6 を展開したとき，x8 の係数を求めよ．	一般項は， 6Ck(2x2)6-k=6Ck26-kx12-2k x8となるのは，12-2k=8 より，k=2のとき．このとき係数は， 6C224=240
(3) $\sum_{k=0}^n_nC_k=2^n$ となることを示せ．	(1 + x)n=nC0+nC1x+nC2x2+…+nCn-1xn-1+nCnxn に x=1を代入すると， 2n=nC0+nC1+nC2+…+nCn-1+nCn となる．
(4)　 $\sum_{k=0}^nk_nC_k=n2^{n-1}$ となることを示せ．	(1 + x)n=nC0+nC1x+nC2x2+…+nCn-1xn-1+nCnxn の両辺を xで微分すると， n(1 + x)n-1=nC1+2nC2x+…+knCkxk-1+…+nnCnxn-1 x=1を代入すると， n2n-1=nC1+2nC2+…+knCk+…+nnCn
短答問題 (1)　　(2x - y)7 を展開したとき，x4y3 の係数を求めよ．	(2)　(x2 - 3)6 を展開したとき，x6 の係数を求めよ．
(3) (1 + x)n=nC0+nC1x+nC2x2+…+nCn-1xn-1+nCnxn の両辺を xで２回微分して，x=1を代入することにより，次の式を簡単にせよ．（右の選択肢の番号［半角数字］で答えよ．） 2·1·nC1+3·2·nC2+…+k(k-1)nCn-k+…+n(n-1)nCn	1　2n-1　　　　　2　2n　　　　　3　2n+1 4　n2n-1　　　　5　(n-1)2n-2　　　　6　(n+1)2n 7　(n+1)n2n-2　　　8　n(n-1)2n-2　　　9　n22n-1 10　　　　11　　　　12
(4) (1 + x)n=nC0+nC1x+nC2x2+…+nCn-1xn-1+nCnxn の両辺を xについて0 から 1まで積分することにより，次の式を簡単にせよ．（右の選択肢の番号［半角数字］で答えよ．） + + + …+

○･･･メニューに戻る