◇定積分の計算◇

== 定積分の計算 ==

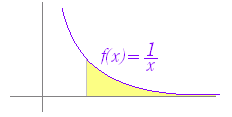
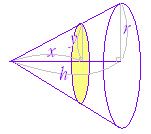
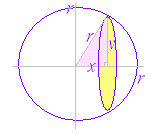
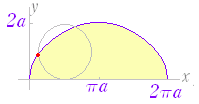
◇微積分学の基本定理◇

　F’(x)=f(x)が成り立つとき，関数F(x)を関数f(x)の原始関数という．このとき，次の関係が成立する．

【微積分学の基本定理】
$\underset{\small a}{\int^b}f(x)dx=F(b)-F(a)$

（証明）
　１次の近似式 F(xk)−F(xk−1)=F ’(ck)Δxk=f(ck)Δxk
（xk−1≦ck≦xk）において，|Δxk| の最大値 |Δ|→0 のとき，ck→xk に注意すると，
(左辺) $=\lim_{\mid\Delta\mid\rightarrow 0}\sum_{k=1}^nf(c_k)\Delta x_k$
$=\lim_{\mid\Delta\mid\rightarrow 0}\sum_{k=1}^n\{F(x_k)-F(x_{k-1})\}$
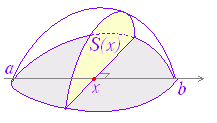
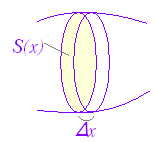
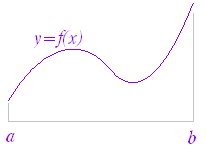
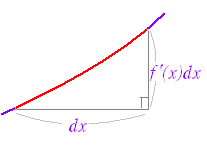
$=\lim_{\mid\Delta\mid\rightarrow 0}\sum_{k=1}^nF(x_k)-\lim_{\mid\Delta\mid\rightarrow 0}\sum_{k=1}^nF(x_{k-1})$
図のように，中央部分が消え両端だけが残るから，
（左辺）=F(xn)−F(x0)=F(b)−F(a)　（証明終）

※　なぜこの関係が「基本定理」なのか？

　もともと定積分（左辺）は，総和の極限として定義されており，直接計算すれば大変な計算量となる．
$\lim_{\mid\Delta\mid\rightarrow 0}\sum_{k=1}^nf(c_k)\Delta x_k$
　これに対して，微分は平均変化率の極限として定義され，
$F\apos(x)=\lim_{h\rightarrow 0}\frac{F(x+ h)-F(x)}{h}$

例えば，(x2)’=2x だから，その逆計算は 2x → x2 のような簡単な式の変形である．

　この２つが等しいことが発見され，総和の極限は微分の逆計算により簡単に求められるようになった．このように，17〜18世紀のニュートンやライプニッツによる微積分学の基本定理の発見は，もともと別の道を歩んできた「積分」と「微分」を結びつけた大きな一歩となっている．（高校では，積分は微分の逆計算として導入されることが多いが，これは微積分学の基本定理のおかげである．）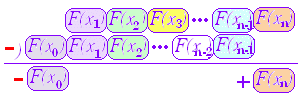

◇不定積分とは◇

○　関数 f(x) の原始関数は，不定積分とも呼ばれ
$\int f(x)dx$
で表わされるが，次のように積分区間の上端が変数xとなる定積分に等しい．

$\underset{\small c}{\int^x}f(x)dx$ （cは任意の定数）
任意の定数c を省略すると， $\int^x f(x)dx$
これを， $\int f(x)dx$ と書く．

○　１つの関数に対する原始関数はただ一つではないが，それらの差は定数である．したがって，原始関数を１つ見つけると他の原始関数も求まる．（任意定数 C を足せばよい．）･･･（＊→）

（＊→）
関数 f(x) の２つの原始関数を F(x)，G(x) とすると，
F ’(x)=f(x)，G ’(x)=f(x) となり，
(F(x)−G(x))’=f(x)−f(x)=0
ゆえに，F(x)−G(x)=C （C は定数）

○　基本的な関数の不定積分

関数 f(x)=F’(x)	不定積分 $F(x)=\int f(x)dx$ (任意定数Cを付けて使う)
定数 $k$	$kx+ C$
$x^k$ (ただし， $k\ne -1$ )	$\frac{x^{k+ 1}}{k+ 1}+ C$
$\frac{1}{x}$	$\log \mid x\mid+ C$
$\sin x$	$-\cos x+ C$
$\cos x$	$\sin x+ C$
$e^x$	$e^x+ C$

（簡単な例）

１次関数
f(x)=ax+b→ $\int f(x)dx=\frac{a}{2}x^2+ bx+ C$
２次関数
f(x)=px2+qx+r
→ $\int f(x)dx=\frac{p}{3}x^3+\frac{q}{2}x^2+ rx+ C$
三角関数
f(x)=sin(2x+3)→ $\int f(x)dx=-\frac{1}{2}\cos(2x+ 3)+ C$
f(x)=cos(2x+3)→ $\int f(x)dx=\frac{1}{2}\sin(2x+ 3)+ C$
指数関数
f(x)=e2x+3→ $\int f(x)dx=\frac{1}{2}e^{2x+ 3}+ C$

◇部分積分法◇
　部分積分法は，積の微分法の逆計算で，元の形では不定積分を求めにくいときに，部分積分法を使えば計算しやすい形に変ることがある．

【不定積分】
$\int uv\apos dx=uv-\int uv\apos dx$ 【定積分】
$\underset{\small a}{\int^b}uv\apos dx=\Bigl[uv\Bigr]_a^b-\underset{\small a}{\int^b}uv\apos dx$

（部分積分法の証明）
【不定積分】
　積の微分法により， (uv)’=u’v+uv’ この式の両辺を x で積分すると $uv=\int u\apos vdx+\int uv\apos dx$ 移項すると，
$\int u\apos vdx=uv-\int uv\apos dx$
【定積分】 (uv)’=u’v+uv’ の両辺を区間 a≦x≦b で積分すると
$\Bigl[uv\Bigr]_a^b=\underset{\small a}{\int^b}u\apos vdx+\underset{\small a}{\int^b}uv\apos dx$ 移項すると，
$\underset{\small a}{\int^b}u\apos vdx=\Bigl[uv\Bigr]_a^b-\underset{\small a}{\int^b}uv\apos dx$

◇置換積分法◇
　置換積分法は，合成関数の微分法の逆計算で，元の形では不定積分を求めにくいときに，置換積分法を使えば計算しやすい形に変ることがある．

【不定積分】x=g(t) とおくと
$\int f(x)dx=\int f\left(g(t)\right)g\apos(t)dt$ 【定積分】x=g(t)とおくとき，a=g(α)，b=g(β)ならば
$\underset{\small a}{\int^b}f(x)dx=\underset{\small \alpha}{\int^{\beta}}f\left(g(t)\right)g\apos(t)dt$

※　実際の計算を行うには，この公式を暗記するのでなく，被積分関数，積分変数，（定積分の場合は積分区間）の各々を等しいものに変換すればよい．（右の例参照）

※不定積分で置換積分法を用いるときは，求まった関数を元の変数で表わしておく．

例
$\int(2x+ 1)^3dx$

2x+1=t とおくと，
　　　被積分関数は，(2x+1)3=t3
　　　=2 だから dx=

$\int(2x+ 1)^3dx=\int t^3\cdot\frac{dt}{2}=\frac{1}{2}\cdot\frac{t^4}{4}+ C$

　tとおいたのは，答案作成者の都合であって，問題文にはそのようなことは書かれていない．
　不定積分の置換積分では，元の変数に戻さなければならない．

$=\frac{(2x+ 1)^4}{8}+ C$ …(答)

※定積分で置換積分法を用いるときは，積分区間が変換され，結果は新しい積分区間の下端と上端 α，β を用いた数値となるので，変数を何にするかということは考えなくてもよい．

例
$\underset{\small 0}{\int^1}(2x+ 1)^3dx$

2x+1=t とおくと，x=0→1 のとき，t=1→3
　　　被積分関数は，(2x+1)3=t3
　　　=2 だから dx=

$\underset{\small 0}{\int^1}(2x+ 1)^3dx=\underset{\small 1}{\int^3}t^3\cdot\frac{dt}{2}$
$=\Bigl[\frac{t^4}{8}\Bigr]_1^3=\frac{81}{8}-\frac{1}{8}=10$ …(答)
※定積分では，値を求めることができればよく，「元の変数が何であったのかは関係ない」

◇広義積分◇

　積分区間の下端または上端が−∞，∞となる定積分を次のように定め，広義積分という．

$\underset{\small a}{\int^{\infty}}f(x)dx=\lim_{b\rightarrow\infty}\underset{\small a}{\int^b}f(x)dx$ …(1)

$\underset{\small -\infty}{\int^{b}}f(x)dx=\lim_{a\rightarrow-\infty}\underset{\small a}{\int^b}f(x)dx$ …(2)

$\underset{\small -\infty}{\int^{\infty}}f(x)dx=\lim_{\underset{a\rightarrow-\infty}{b\rightarrow\infty}}\underset{\small a}{\int^b}f(x)dx$ …(3)
ただし，(3)では，a→−∞ と b→∞ の２つの極限は分けて考えて，
$\underset{\small -\infty}{\int^{0}}f(x)dx,\hspace{10}\underset{\small 0}{\int^{\infty}}f(x)dx$ が両方とも存在するときにその和で定義されるものとすればよい．

(1)の広義積分が有限確定値となるためには，x→∞のときf(x)→0でなければならない（必要）が，f(x)→0であっても $\underset{\small a}{\int^{x}}\frac{1}{x}dx=\log x-\log a\rightarrow\infty$ のように無限大に発散するものもある．

f(x)=xk の形の関数については，
ア） k<−1 のときは，
$\underset{\small a}{\int^{\infty}}f(x)dx=\lim_{x\rightarrow\infty}\left(\frac{x^{k+ 1}}{k+ 1}-\frac{a^{k+ 1}}{k+ 1}\right)$
は有限確定値となるが，
イ） k>−1 のときは，
$\underset{\small a}{\int^{\infty}}f(x)dx=\lim_{x\rightarrow\infty}\left(\frac{x^{k+ 1}}{k+ 1}-\frac{a^{k+ 1}}{k+ 1}\right)$
は無限大に発散する．
ウ） k=−1 のときは，上記のように，log x−log aとなって無限大に発散する．（k=−1 が境目となっている．）

　問題　
（半角数字=1バイト文字で答えよ）

(1)　(−e−∞)−(−e0)=0+1=1
(2)　（原式）=log 1−log=0−(−log 2)=log 2

２．　−∞<x<∞ で定義される確率密度関数（統計では確率分布関数と呼ばれることが多い） f(x) は，任意の x に対して f(x)≧0 となる他，全事象の確率が1となることに対応して，次の条件を満たさなければならない．

◇立体の体積◇

　図１のような立体を x 軸に垂直な平面で切ったときの断面積を S(x) とすると，区間 a≦x≦b にある立体の体積は，
$V=\underset{\small a}{\int^{b}}S(x)dx$ で求められる．

（解説）
　円柱や角柱などの柱状図形の体積は，(底面積)×(高さ)で求められ，図２のように高さΔxを x 軸方向に，x 軸に垂直な断面を底面積に選ぶと，この薄い柱状図形の体積は

ΔV_k=S(x_k)Δx_k

となる．

a=x₀<x₁<x₂<···<x_n=b

で分割されたｎ個の区間について，これらの総和を求めると，

$\sum_{k=1}^n\Delta V_k=\sum_{k=1}^nS(x_k)\Delta x_k$

さらに，分割を細かくして，Δx_k の最大値 |Δ| を限りなく 0 に近づけると，

$V=\lim_{\mid\Delta\mid\rightarrow 0}\sum_{k=1}^n\Delta V_k=\lim_{\mid\Delta\mid\rightarrow 0}\sum_{k=1}^nS(x_k)\Delta x_k$

は，定積分で表わすことができ，

$V=\underset{\small a}{\int^b}S(x)dx$

となる．

図１

図２

注意
　S(x) が断面積であっても，次の図のように断面が x 軸に垂直でなければ，
$\underset{\small a}{\int^b}S(x)dx$ は体積を表わさない．

　x 軸に垂直に切ったときの断面積を，x 座標の関数として表わすことが重要である．

　図３のように，y=f(x) のグラフと x 軸，x=a , x=b の直線で囲まれる図形を x 軸のまわりに回転してできる回転体の体積は，
$V=\pi\underset{\small a}{\int^b}\{f(x)\}^2dx$ で求められる．

（解説）
x軸に垂直な断面積はS(x)=π{f(x)}²
となり，これを積分すれば得られる．

例　y=x² の曲線と x 軸，x=0 , x=1 の直線で囲まれる図形を x 軸のまわりに回転してできる回転体の体積は，

$V=\pi\underset{\small 0}{\int^1}(x^2)^2dx=\frac{\pi}{5}$ 　なお，図４のようにドーナツ状に中空があるときは，中空の部分を取り除く．
　図5のように x 軸の両側にある図形を回転するときは，x 軸から最も遠い線（図では赤の破線）が残る．

図3

図４

図５

　問題　

◇曲線の長さ◇

○　区間 a≦x≦b における曲線 y=f(x) の長さを L とすると

$L=\underset{\small a}{\int^b}\sqrt{1+\{f\apos(x)\}^2}dx$

○　区間α≦t≦βにおいて媒介変数tを用いて定義される曲線

	x=f(t)
	y=g(t)

の曲線の長さを L とすると

$L=\underset{\small \alpha}{\int^{\beta}}\sqrt{\{f\apos(t)\}^2+\{g\apos(t)\}^2}\hspace{5}dt$

（解説）
xの増分dxに対するyの増分をdyとすると，

dy=f’(x)dx

だから，この微小区間dxにおける曲線の長さdLは，ピタゴラスの定理により

$dL=\sqrt{(dx)^2+(dy)^2}$
$=\sqrt{(dx)^2+\{f\apos(x)dx\}^2}$
$=\sqrt{1+\{f\apos(x)\}^2}dx$

両辺を区間a≦x≦bにおいて積分すると，

$L=\underset{\small a}{\int^{b}}\sqrt{1+\{f\apos(x)\}^2}dx$

例
　曲線 y=　（0≦x≦1）の長さを求めよ．
（答案）
　y’=
だから
$L=\underset{\small 0}{\int^{1}}\sqrt{1+(y\apos)^2}dx=\underset{\small 0}{\int^{1}}\sqrt{1+(\frac{e^x-e^{-x}}{2})^2}dx$
$=\underset{\small 0}{\int^{1}}\sqrt{4+\frac{e^{2x}-2+ e^{-2x}}{4}}dx$
$=\underset{\small 0}{\int^{1}}\sqrt{\frac{e^{2x}+ 2+ e^{-2x}}{4}}dx$ $=\underset{\small 0}{\int^{1}}\sqrt{\{\frac{e^{x}+ e^{-x}}{2}\}^2}dx$
$=\underset{\small 0}{\int^{1}}\frac{e^{x}+ e^{-x}}{2}dx=\Bigl[\frac{e^{x}-e^{-x}}{2}\Bigr]_0^1$
$=\frac{e-\frac{1}{e}}{2}-\frac{1-1}{2}=\frac{1}{2}(e-\frac{1}{e})$

※曲線の方程式が媒介変数で表わされているときは，

$dL=\sqrt{(dx)^2+(dy)^2}$
$=\sqrt{\{f\apos(t)dt\}^2+\{g\apos(t)dt\}^2}$
$=\sqrt{\{f\apos(t)\}^2+\{g\apos(t)\}^2}dt$

より，

$L=\underset{\small \alpha}{\int^{\beta}}\sqrt{\{f\apos(t)\}^2+\{g\apos(t)\}^2}\hspace{5}dt$

が得られる．

例
　半径が a の円を直線上で滑ることなく回転させたとき，円周上の１点が描く軌跡はサイクロイド曲線と呼ばれ，

x=a(t−sin t), y=a(1−cos t) （0≦t≦2π，a>0）

で表わされる．
　この曲線の長さを求めよ．

（答案）
=a(1−cos t) , =asin t

$L=\underset{\small 0}{\int^{2\pi}}\sqrt{\{a(1-\cos t\}^2+\{a\sin t\}^2}\hspace{5}dt$
$L=\underset{\small 0}{\int^{2\pi}}\sqrt{a^2(1-2\cos t+ 1)}dt$
$L=\sqrt{2}a\underset{\small 0}{\int^{2\pi}}\sqrt{1-\cos t}dt$
半角公式 cos t=1−2sin2 を用い，
0≦t≦2πのとき0≦≦π に注意すると， sin≧0
$L=2a\underset{\small 0}{\int^{2\pi}}\sin\frac{t}{2}dt=-4a\Bigl[\cos\frac{t}{2}\Bigr]_0^{2\pi}=8a$

※円周の長さには， 2πa という形で無理数πが登場するが，サイクロイドの長さは，半径の整数倍 L=8a となるのは興味深い．なお，サイクロイドの面積は円の３倍になる：S=3πa²

○===メニューに戻る