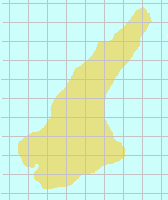
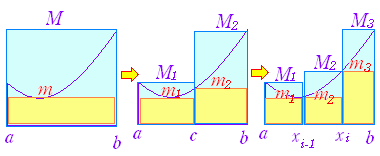
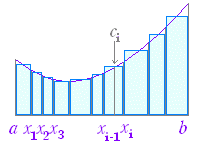
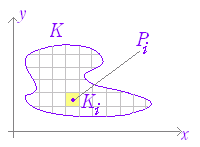
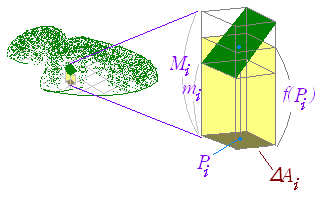
◇面積とは何か◇(考え方の要点)A は2次元の図形,m(A) は図形にその面積を対応させる関数とするとき,関数 m(A) は次の性質をもつ. (1) m(A)≧0
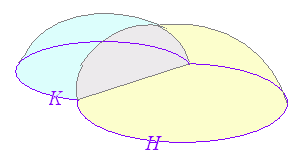
上の性質を前提とすれば,例えば次のような常(2) m( (3) A∩B= 面積を表わす関数 m(A) は,さらに次の性質を持つものとする: (4) 長方形 R については,m(R)=ab 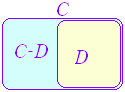 識(?)も証明可能な定理となる. 識(?)も証明可能な定理となる.「C⊃D ならば m(C)≧m(D)」 (∵) 集合 C のうち D でないものを C−D で表わす.(参考までに,C+D という記号は使わず,和集合は C (C−D)∩D= m(C)=m(C−D)+m(D) m(C)−m(D)=m(C−D)≧0 |
○ 左の性質(1)(2)(3)を満たすものの例
A を事象とし,p(A) を事象 A が起こる確率とすると,  ○ 左の性質でA は3次元の図形,m(A) は図形にその体積を対応させる関数とするとき,(4)は次の形になる. ○ 左の性質でA は3次元の図形,m(A) は図形にその体積を対応させる関数とするとき,(4)は次の形になる.(4) 直方体 R については,m(R)=abc |