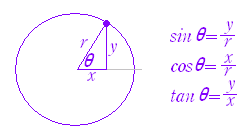|
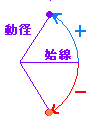
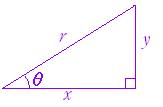
小学校以来,角度の単位には円の一周を360°とする60分法に慣れているが,微分積分では,次に述べる弧度法の単位(ラジアン)を用いる. 右の図1のように,2つの相似図形では対応する辺の長さの比が等しいので「弧の長さ/半径」の比は,図形の大きさによらず扇形の角度だけで決まる. そこで,弧度法では θ = =
を角度の定義とする.(単位はラジアン.ただし,ラジアンは省略してよい.) |
図1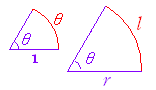
|
||||||||||||||||||
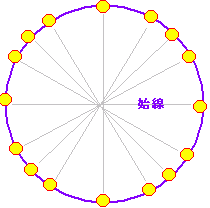
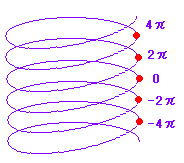
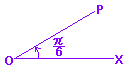
| 右の図2のように,角度を2倍,3倍,... とすると弧の長さも2倍,3倍,... となり,弧の長さと角度は比例するので,60分法の角度を弧度法の角度に直すには,円周の長さから比例計算で求めるとよい. 図3のように,360°=2 (幾つかの例)
|
図2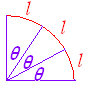 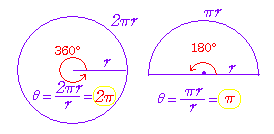 |