→ スマホ版は別頁

■数集合と演算

○　自然数

　ものの個数や順序を数えるには，自然数（正の整数）
1，2，3，···，100，···　
だけで十分である．

○　任意の２つの自然数の和や積は，自然数となる．このとき，自然数は和，積の演算について閉じているという．
［記号］　a が集合M の要素であることを，a∈M と書く．
　　　　　 b が集合M の要素でないことを，b∈/M と書く．

　 自然数全体の集合を N で表わす．すなわち，
N={1，2，3，··· }　
とするとき，
x，y∈N　ならば　x+y∈N
x，y∈N　ならば　xy∈N
が成り立つ．

　これに対して，自然数全体の集合は差の演算については，閉じていない．例えば，3−5 は自然数にならない．
　 　x，y∈N　ならば　x−y∈N は必ずしも成り立たない．
　　　例：x=3，y=5　のとき　x−y∈/ N



※　「閉じていないとき」演算の結果が集合の外に出るような要素 x，y が少なくとも１つ存在する．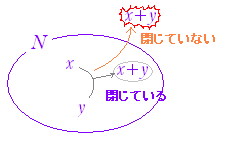
※　「閉じている」といえるためには，任意の２つの要素について，演算の結果が元の集合に含まれることを要す．したがって，成り立つ例が何個あっても，成り立たない例が１つでもあれば閉じていないこととなる．
「すべてのxについてp(x)が成り立つ」の否定は，「あるx についてp(x)が成り立たない」である．

簡単な例：
「この教室にいるのは全員男子である」という主張が間違っていることを示すには，「この教室にいるのは全員女子である」ことを示す必要はない．「この教室に女子が（少なくとも）１人いる」ことを示せばよい．
○　整数

　自然数から任意の２つの要素を選んで，差の演算について閉じているようにするには，
　5−5 = 0
3−5 =−2
のような場合に対応するため，零( 0)と負の整数も含めた整数の集合に拡張すればよい．

　整数全体の集合は差の演算について閉じている．
　整数全体の集合を Z で表わす．すなわち，
Z={···，−2，−1，0，1，2，3，··· }　
とするとき，
x，y∈Z　ならば　x−y∈Z
が成り立つ．

　Z は，和，積，差の演算について閉じている．
○　有理数

　整数から任意の２つの要素を選んで，商の演算を行うと，必ずしも整数とはならない．（ただし，0で割ることは考えないものとする．）
　整数から任意の２つの要素を選んで，0で割ることを除く商の演算について閉じているようにするためには，

5 ÷ 3 =

のような場合に対応するため，整数と分数を合わせた有理数の集合に拡張すればよい．

　有理数全体の集合は商の演算について閉じている．

　有理数は，整数（分母が分子の約数であるもの）または分数（分母が分子の約数でないもの）となるので，整数，有限小数，循環小数となる．
 ※　有理数とは，整数÷整数で表わされる数のことで，特に分母が1となる場合（整数）も含まれる．
　有理数全体の集合を Q で表わす．すなわち，

Q={ | m, n∈Z , n≠0 }　
とするとき，
x，y∈Q 　(y≠0)　ならば　∈Q
が成り立つ．

　Qは，和，差，積，商の四則演算について閉じている．

集合の表し方は２種類ある．

(1)　要素を書き並べる方法
　　　例　A={2，4，6，8 }，N={1，2，3，··· }

(2)　要素と条件で表わす方法
　　　　{ 要素 | 条件} の形で書く．
　　　条件が複数個あるときは
　　　　{ 要素 | 条件，条件，･･･} の形とする．（カンマは「かつ」を表わす．）
　　 例　E={ 2n| n∈Z }，Q={ | m, n∈Z , n≠0 }
○　実数

　a (>0)を有理数とするとき，方程式 x2=a の解は必ずしも有理数とはならない．
　例えば，x2=2 の解は有理数の範囲になく，と書かれる無理数となる．
　この他，円周率 π=3.14··· や自然対数の底 e=2.718···など，循環しない無限小数で表わされるものは無理数と呼ばれる．
　有理数と無理数を合わせたものを実数という．実数全体の集合は，数直線上の点全体に対応する．
　実数全体の集合を R で表わす．
　R は，和，差，積，商の四則演算について閉じている．
○　複素数

　a ，b，c，··· を実数とするとき，a ，b，c，··· を係数とする2次，3次などのn次方程式の解は，必ずしも実数の範囲にない．
　x2=−1 の解は，虚数 x=±i となる．
　実数と虚数を合わせたものを複素数という．複素数を係数とするn次方程式の解は，複素数の範囲にあり，複素係数のn次方程式を解く上で，複素数よりも広い範囲の数は必要ない．
　 　複素数全体の集合を C で表わすと，
C={ a+bi| a, b∈R , i2=−1}　
となる．
　C は，和，差，積，商について閉じている．
　また，C の要素を係数とするn次方程式の解はC の要素となる．
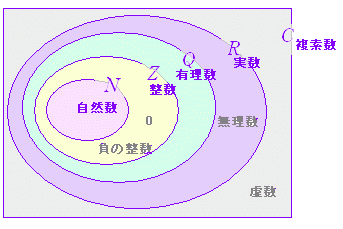
◇まとめ◇

　ここで登場した数集合の包含関係は右図のようになる．
  • N⊂Z⊂Q⊂R⊂C が成り立つ．
  • 複素数のうち実数でないものが虚数(a+bi ，b≠0 のもの)
  • 実数のうち有理数でないものが無理数
  • 有理数のうち整数でないものが分数
  • 整数のうち自然数でないものが負の整数と0
　負または0の整数の和を除けば，虚数，無理数，分数，負または0の整数の集合は，和差積商のどの演算についても閉じていない．
i+(−i)=0∈R , i×i=−1∈R



+(−)=0∈Z , ×=1∈Z

(−2)−(−5)=3∈N , (−2)×(−2)=4∈N
※　以下の問題においては，上の解説で取り扱った程度の証明を想定する．（例えば，このページでは，「自然数とは何か」を定義をしていないので，自然数の和が自然数になることの証明は扱っていない．）
例と答

(1)　奇数全体の集合をA で表わすとき，集合A は差の演算について閉じていないことを示せ．

 （答案）
A={2n+1 | n∈Z }
x，y∈A ならば，x=2m+1 , y=2n+1 と書ける．
このとき，x−y =(2m+1)−(2n+1)=2(m−n)∈/ A
(2)　有理数全体の集合は商の演算について閉じていることを示せ．ただし，0で割ることは除く． （答案）
Q={ | m, n∈Z , n≠0 }

x，y∈Q ，y≠0 ならば，

x= 　(p, q∈Z , q≠0)

y=　 (r, s∈Z , r, s≠0)と書ける．

このとき，x ÷ y =　 (ps∈Z , qr∈Z, qr≠0) だから
x ÷ y∈Q
(3)　複素数全体の集合は積の演算について閉じていることを示せ． （答案）
C={ a+bi| a, b∈R , i2=−1}
x，y∈C ならば，x=a+bi , y=c+di , i2=−1と書ける．
このとき，
xy=(a+bi)(c+di)=ac+adi+bci+bdi2
=(ac−bd)+(ad+bc)i
ここで，ac−bd，ad+bc∈R だから xy∈C
(4)　「無理数全体の集合は，差について閉じている」という命題が正しくないことを示す反例を１つあげよ． （答案）
実数のうち有理数でないものを無理数という．
は有理数となる．
(5)　集合は，和の演算について閉じていることを示せ． （答案）
x，y∈A ならば，と書ける．
このとき，


■即答問題■

　次の問に答えよ．
(1)　3の倍数全体の集合 T={ 3n| n∈Z}が積の演算について閉じているかどうか調べよ．

＜閉じている | 閉じていない＞
 (3)　集合 （は有理数全体の集合）が差の演算について閉じているかどうか調べよ．

＜閉じている | 閉じていない＞
(2)　奇数全体の集合 S={ 2n+1| n∈Z}が商の演算について閉じているかどうか調べよ．

＜閉じている | 閉じていない＞
 (4)　複素数全体の集合が商の演算について閉じているかどうか調べよ．（ただし，0で割ることは除く）

＜閉じている | 閉じていない＞

○･･･メニューに戻る