|
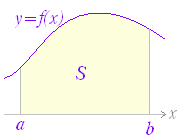
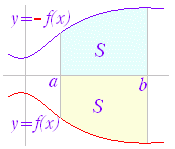
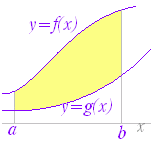
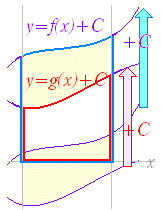
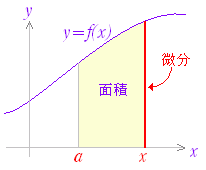
関数 F(x)の微分がf(x)のとき,f(x)の不定積分はF(x)+Cと表せる.すなわち, ○ 曲線で囲まれた図形の面積 図1のように,区間a≦x≦b において,曲線y=f(x)とx軸とで囲まれる図形の面積を求めるにはどうすればよいか. 図1の面積Sを直接求める代わりに,Sの微分を求めることを考える.上の復習で分かるように,ある関数の微分が分かれば,元の関数はその不定積分で求められるからである. 図2のように,区間の右端を変数xとして,この区間において,曲線とx軸とで囲まれる図形の面積をS(x)とおく. ただし,曲線y=f(x)はx軸よりも上にあるものとする. 図3のように S(x)の増分ΔSを考えると,図4からΔSは小さい長方形と大きい長方形の間にあるから, f(x)<<f(x+Δx)
Δx→0 の極限により,微分を求めると,f(x)≦≦f(x+Δx)=f(x)
ゆえに,=f(x)
※ 上で示した方法:
f(x)<g(x)<h(x)かつf(x)=h(x)=k
とする推論の方法を,はさみうち論法という.ならばg(x)=k はさみうち論法において,極限移行前には不等号であっても,一般に極限値には等号が必要となる. すなわち, (簡単な例) x>0のとき,(−x)<0<xであるが,
(−x)≦0≦x
|
図1 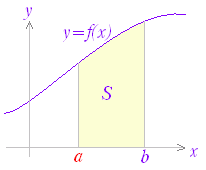 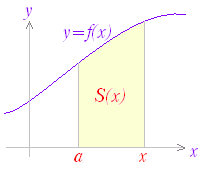 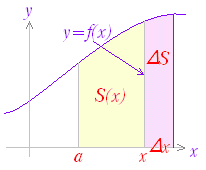 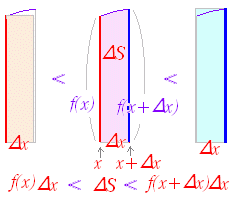 |
||
微分が f(x) になるのだから,S(x) は f(x) の不定積分となる. ここで,右端が左端に一致すれば面積は0となるから, C=−F(a)
|
 |
||
| 例 曲線y=x2(1≦x≦2)とx軸とで囲まれた図形の面積は, ∫ x2dx=+Cに注意すると,−= となる. |
例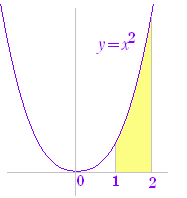 |
||
| ○ 記号と用語 上のように面積の計算をするときは,原始関数の差がつねに登場する. そこで, F(b)−F(a)を
さらに,これを実際に使うときは, |
例 上の例: y=x2 (1≦x≦2) とx軸とで囲まれた図形の面積は, |
||
| ○ 定積分の計算 上の文章では,面積と結びつけて定積分を導入したが,定積分と面積の関係は下で述べる. ここでは,まず,原始関数(不定積分)の差として定積分の計算に慣れることを目指す. 右の手順に沿って,計算すればよい.ただし,不定積分の任意定数は,差で消えるので,付けなくてよい( =0).次の2つの式を比較してみるとよい: これは,次の式と同じになる. |
 ※ この式でaを(定積分の)下端,b を(定積分の)上端という. F(上端)−F(下端)とすることが重要.(逆ではない) |
||
| 例と答 次の定積分を求めよ.
(1)
(解答)
(2)
(解答) |
(3)
(解答)
(4)
(解答) |